
����Ŀ����ÿ�����һСʱ������������ʮ�꣬�Ҹ�����һ����.��һ���е�λΪ�˽�Ա�������˶��Ƿ����Ա��йأ��ӵ�λ�����ȡ30��Ա���������ʾ����飬�õ���������������
���� | Ů�� | �ϼ� | |
���� | 10 | ||
������ | 8 | ||
�ϼ� | 30 |
��֪����30���������ȡ1�˳鵽�����˶���Ա���ĸ�����![]() .
.
��1���뽫����������������������ڴ������ֱ����д���������Ҫд�����̣������ݴ����Ϸ����ܷ��а�����Ϊ�����˶����Ա��йأ�
��2��������30���е�Ů��Ա���������ȡ2�˲μ�һ����ǰ����˶�������Ϊ![]() ����
����![]() �ķֲ��С���ѧ����.�ο����ݣ�
�ķֲ��С���ѧ����.�ο����ݣ�
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡���1��û�а�����Ϊ�����˶����Ա��йأ� ��2��![]() .
.
��������
��1���������������˶����ˣ���������б��������ù�ʽ���![]() ���ɵó������
���ɵó������
��2�����͵ij����ηֲ������ù�ʽ��ø��ʣ��г��ֲ��У��������.
��1��
���� | Ů�� | �ϼ� | |
���� | 10 | 6 | 16 |
������ | 6 | 8 | 14 |
�ϼ� | 16 | 14 | 30 |
����֪���ݿ���ã�
![]()
![]() ��
��
����û�а�����Ϊ�����˶����Ա��йأ�
��2��![]() ��ȡֵ����Ϊ0��1��2��
��ȡֵ����Ϊ0��1��2��
![]() ��
��![]() ��
��
![]() .
.
����![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| 0 | 1 | 2 |
|
|
|
|
![]() ����ѧ����Ϊ
����ѧ����Ϊ
![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,���ⳤ����ȵ�����![]() ��,
��, ![]() �������������,
�������������, ![]() ,
,![]() �ֱ�Ϊ����
�ֱ�Ϊ����![]() ,
,![]() ���е�,�����н�����ȷ���У�( )
���е�,�����н�����ȷ���У�( )

A.![]() ��ƽ��
��ƽ��![]() B.ƽ��
B.ƽ��![]() ��ƽ��
��ƽ��![]()
C.ֱ��![]() ��ֱ��
��ֱ��![]() ���ɽǵĴ�СΪ
���ɽǵĴ�СΪ![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ݣ��ף�12��13��11��10��14.�ң�10��17��10��13��10.
��1���ֱ�����������ݵ�ƽ��������ݼ������ж��������ݲ�����.
��2���ֱ�����������ݵķ�������ݼ������ж��������ݲ�����.
��3�����������жϷ����Ľ���Ƿ�һ�£�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѡ��4-4������ϵ�����������
��ֱ������ϵ![]() ��������
��������![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() Ϊ��������������ԭ��
Ϊ��������������ԭ��![]() Ϊ������
Ϊ������![]() ���������Ϊ���Ὠ��������ϵ������
���������Ϊ���Ὠ��������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
������������![]() �ļ����귽�̺�
�ļ����귽�̺�![]() ��ֱ�����귽����
��ֱ�����귽����
������ֱ��![]() ������
������![]() �ֱ��ڵ�һ�����ڵ�
�ֱ��ڵ�һ�����ڵ�![]() ��
��![]() ���㣬��
���㣬��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ӽס�������ѧ����ѡ��һ�˲μ���������������ǵ����ˮƽ�����˲��ԣ���������ͬ�����¸����10�Σ����еĻ������£�
�ף�7��8��6��9��6��5��9��9��7��4.
�ң�9��5��7��8��7��6��8��6��7��7.
��1���ֱ����ס�������������л����ļ����������λ����
��2���ֱ����ס�������������л�����ƽ������������
��3���Ƚ����˵ijɼ���Ȼ�����ѡ����һ���˲���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����AC��BC��AC=BC=1����P�ǡ�ABC��һ�㣬��![]() ��ȡֵ��Χ�ǣ�������
��ȡֵ��Χ�ǣ�������
A. ����![]() ��0�� B. ��0��
��0�� B. ��0��![]() �� C. ����
�� C. ����![]() ��
��![]() �� D. ����1��1��
�� D. ����1��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���������Ա����ڲ�ͬ��Χ��ȡֵʱ����������ʽ��ͬ�����dz������ĺ���Ϊ�ֶκ������������Dz���ѧϰ�����Ĺ����뷽����̽���ֶκ���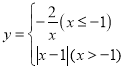 ��ͼ�������ʣ��б���
��ͼ�������ʣ��б���
x | �� |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | �� |
y | �� |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | �� |
��㣺��ƽ��ֱ������ϵ�У����Ա���x��ȡֵΪ�����꣬����Ӧ�ĺ���ֵyΪ�����꣬�����Ӧ�ĵ㣬��ͼ��ʾ��
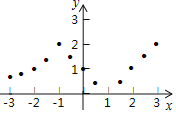
��1����ͼ����ƽ��ֱ������ϵ�У��۲��������Щ��ķֲ�����������ͼ��
��2���о����������ͼ������ش��������⣺
�ٵ�![]() ��
��![]() ��
��![]() ��
��![]() �ں���ͼ���ϣ�
�ں���ͼ���ϣ�![]() �� ��
�� ��![]() ��
��![]() �� ��
�� ��![]() ������������������������������
������������������������������
�ڵ�����ֵ![]() ʱ�����Ա���x��ֵ��
ʱ�����Ա���x��ֵ��
����ֱ��![]() ���Ҳ�ĺ���ͼ������������ͬ�ĵ�
���Ҳ�ĺ���ͼ������������ͬ�ĵ�![]() ��
��![]() ����
����![]() ����
����![]() ��ֵ��
��ֵ��
����ֱ��![]() �뺯��ͼ����������ͬ�Ľ��㣬��a��ȡֵ��Χ��
�뺯��ͼ����������ͬ�Ľ��㣬��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����Ϊ50������,���ݵķ����Լ������Ƶ������:
[12.5,15.5),3;[15.5,18.5),8;[18.5,21.5),9;[21.5,24.5),11;[24.5,27.5),10;[27.5,30.5),5;[30.5,33.5],4.
(1)�г�������Ƶ�ʷֲ���.
(2)����Ƶ�ʷֲ�ֱ��ͼ.
(3)����Ƶ�ʷֲ���,������������[15.5,24.5)�ڵĿ�����Լ�Ƕ���?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com