
选修4-4:坐标系与参数方程已知直线l: (t为参数)恒经过椭圆C:
(t为参数)恒经过椭圆C: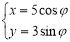 (?为参数)的右焦点F.
(?为参数)的右焦点F.
(Ⅰ)求m的值;
(Ⅱ)设直线l与椭圆C交于A,B两点,求|FA|·|FB|的最大值与最小值.
(Ⅰ)4;(Ⅱ)最大值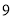 ,最小值
,最小值
【解析】
试题分析:(Ⅰ)将椭圆的参数方程化为普通方程得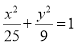 ,易求其右焦点为
,易求其右焦点为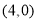 ,因为直线直线
,因为直线直线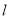 经过点
经过点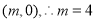 ;(Ⅱ)在标准直线参数方程中,
;(Ⅱ)在标准直线参数方程中,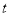 的几何意义是
的几何意义是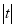 表示直线上的点到定点
表示直线上的点到定点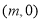 的距离,故将直线参数方程带入椭圆普通方程得
的距离,故将直线参数方程带入椭圆普通方程得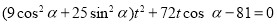 ,则
,则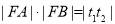 ,利用韦达定理用参数将目标函数用
,利用韦达定理用参数将目标函数用 表示,转化为三角函数的最值问题处理.
表示,转化为三角函数的最值问题处理.
试题解析:(Ⅰ)椭圆的参数方程化为普通方程,得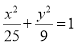 ,
,
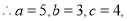 则点
则点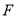 的坐标为
的坐标为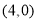 .
.
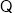 直线
直线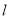 经过点
经过点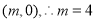 . (4分)
. (4分)
(Ⅱ)将直线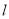 的参数方程代入椭圆
的参数方程代入椭圆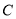 的普通方程,并整理得:
的普通方程,并整理得:
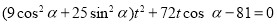 .
.
设点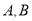 在直线参数方程中对应的参数分别为
在直线参数方程中对应的参数分别为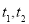 ,则
,则
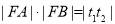 =
= (8分)
(8分)
当 时,
时,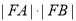 取最大值
取最大值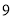 ;
;
当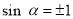 时,
时,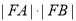 取最小值
取最小值 (10分)
(10分)
考点:1、直线和椭圆的参数方程;2、直线参数方程中参数的几何意义.


科目:高中数学 来源:2015届河南省顶级名校高三入学定位考试文科数学试卷(解析版) 题型:填空题
设O是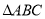 的三边中垂线的交点,
的三边中垂线的交点,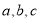 分别为角
分别为角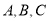 对应的边,已知
对应的边,已知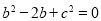 ,则
,则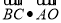 的范围是___________.
的范围是___________.
查看答案和解析>>
科目:高中数学 来源:2015届河南省开封市高三上学期定位模拟考试理科数学试卷(解析版) 题型:选择题
设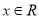 ,若函数
,若函数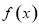 为单调递增函数,且对任意实数
为单调递增函数,且对任意实数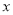 ,都有
,都有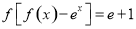 (
(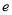 是自然对数的底数),则
是自然对数的底数),则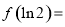 ( )
( )
A.1 B.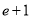 C.3 D.
C.3 D.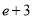
查看答案和解析>>
科目:高中数学 来源:2015届河南省开封市高三上学期定位模拟考试文科数学试卷(解析版) 题型:选择题
三棱柱 侧棱与底面垂直,体积为
侧棱与底面垂直,体积为 ,高为
,高为 ,底面是正三角形,若
,底面是正三角形,若 是
是 中心,则
中心,则 与平面
与平面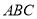 所成的角大小是( )
所成的角大小是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届河南省开封市高三上学期定位模拟考试文科数学试卷(解析版) 题型:选择题
对一个容量为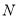 的总体抽取容量为
的总体抽取容量为 的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为
的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为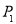 、
、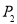 、
、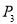 ,则( )
,则( )
A. B.
B.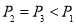 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届河南省名校高三上学期期中理科数学试卷(解析版) 题型:解答题
设函数
(1)求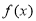 的最大值,并写出使
的最大值,并写出使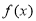 取最大值时x的集合;
取最大值时x的集合;
(2)已知 中,角A、B、C的对边分别为a、b、c,若
中,角A、B、C的对边分别为a、b、c,若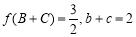 ,求a的最小值.
,求a的最小值.
查看答案和解析>>
科目:高中数学 来源:2015届河南省名校高三上学期期中理科数学试卷(解析版) 题型:选择题
如图,把周长为1的圆的圆心C放在y轴上,顶点A(0,1),一动点M从A开始逆时针绕圆运动一周,记弧AM=x,直线AM与x轴交于点N(t,0),则函数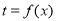 的图像大致为( )
的图像大致为( )
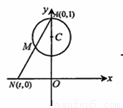
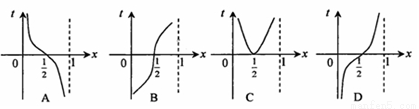
查看答案和解析>>
科目:高中数学 来源:2015届河南省名校高三上学期期中文科数学试卷(解析版) 题型:选择题
设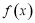 是定义在R上的偶函数,且对于
是定义在R上的偶函数,且对于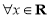 恒有
恒有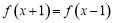 ,已知当
,已知当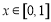 时,
时,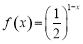 则
则
(1)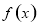 的周期是2;
的周期是2;
(2)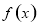 在(1,2)上递减,在(2,3)上递增;
在(1,2)上递减,在(2,3)上递增;
(3)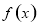 的最大值是1,最小值是0;
的最大值是1,最小值是0;
(4)当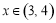 时,
时,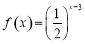
其中正确的命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2015届河南省八校高三上学期第一次联考文科数学试卷(解析版) 题型:解答题
已知圆C的极坐标方程为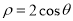 ,直线l的参数方程为
,直线l的参数方程为 (t为常数,t∈R)
(t为常数,t∈R)
(Ⅰ)求直线l的普通方程和圆C的直角坐标方程;
(Ⅱ)求直线l与圆C相交的弦长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com