
已知圆C的极坐标方程为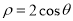 ,直线l的参数方程为
,直线l的参数方程为 (t为常数,t∈R)
(t为常数,t∈R)
(Ⅰ)求直线l的普通方程和圆C的直角坐标方程;
(Ⅱ)求直线l与圆C相交的弦长.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015届河南省名校高三上学期期中理科数学试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程已知直线l: (t为参数)恒经过椭圆C:
(t为参数)恒经过椭圆C: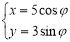 (?为参数)的右焦点F.
(?为参数)的右焦点F.
(Ⅰ)求m的值;
(Ⅱ)设直线l与椭圆C交于A,B两点,求|FA|·|FB|的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源:2015届河南省名校高三上学期期中文科数学试卷(解析版) 题型:选择题
设f(x)是定义在R上的奇函数,当 时,f(x)=x
时,f(x)=x (e为自然对数的底数),则
(e为自然对数的底数),则 的值为 ( )
的值为 ( )
A.ln6+6 B. ln6-6 C. -ln6+6 D.-ln6-6
查看答案和解析>>
科目:高中数学 来源:2015届河南省八校高三上学期第一次联考理科数学试卷(解析版) 题型:选择题
已知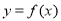 为R上的连续可导函数,当x≠0时
为R上的连续可导函数,当x≠0时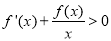 ,则函数
,则函数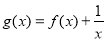 的零点个数为( )
的零点个数为( )
A.1 B.2 C.0 D.0或2
查看答案和解析>>
科目:高中数学 来源:2015届河南省八校高三上学期第一次联考理科数学试卷(解析版) 题型:选择题
设 在(-∞,+∞)上单调递增;
在(-∞,+∞)上单调递增; ,则p是q的( )
,则p是q的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.以上都不对
查看答案和解析>>
科目:高中数学 来源:2015届河南省八校高三上学期第一次联考文科数学试卷(解析版) 题型:解答题
抛掷一枚质地不均匀的骰子,出现向上点数为1,2,3,4, 5, 6的概率依次记为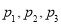 ,
,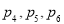 ,经统计发现,数列
,经统计发现,数列 恰好构成等差数列,且
恰好构成等差数列,且 是
是 的3倍.
的3倍.
(Ⅰ)求数列 的通项供式;
的通项供式;
(Ⅱ)甲、乙两人用这枚骰子玩游戏,并规定:掷一次骰子后,若向上点数为奇数,则甲获胜,否者乙获胜,请问这样的规则对甲、乙二人是否公平,请说明理由;
(Ⅲ)甲、乙丙三人用这枚骰子玩游戏,根据掷一次后向上的点数决定胜出者,并制定了公平的游戏方案,试在下面的表格中列举出两种可能的方案(不必证明)
方案序号 | 甲胜出对应点数 | 乙胜出对应点数 | 丙胜出对应点数 |
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源:2015届河南省八校高三上学期第一次联考文科数学试卷(解析版) 题型:选择题
已知函数 的两个极值分别为
的两个极值分别为 和
和 .若
.若 和
和 分别在区间(-2,0)与(0,2)内,则
分别在区间(-2,0)与(0,2)内,则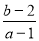 的取值范围为( )
的取值范围为( )
A. B.
B.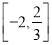
C. D.
D.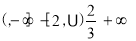
查看答案和解析>>
科目:高中数学 来源:2015届河南省原名校高三上学期第一次摸底考试数学理科数学试卷(解析版) 题型:解答题
设X为随机变量,从棱长为a的正方体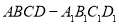 ,的八个顶点中任取四个点,当四点共面时,X=0;当四点不共面时,X的值为四点组成的四面体的体积.
,的八个顶点中任取四个点,当四点共面时,X=0;当四点不共面时,X的值为四点组成的四面体的体积.
(1)求概率P(X=0);
(2)求X的分布列,并求其数学期望E(X).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com