
设函数
(1)求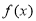 的最大值,并写出使
的最大值,并写出使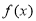 取最大值时x的集合;
取最大值时x的集合;
(2)已知 中,角A、B、C的对边分别为a、b、c,若
中,角A、B、C的对边分别为a、b、c,若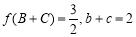 ,求a的最小值.
,求a的最小值.
科目:高中数学 来源:2015届河南省顶级名校高三入学定位考试文科数学试卷(解析版) 题型:选择题
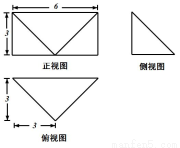
如图是一个几何体的三视图,则该几何体的体积是( )
(A)54 (B)27 (C)18 (D) 9
查看答案和解析>>
科目:高中数学 来源:2015届河南省名校高三上学期期中理科数学试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程已知直线l: (t为参数)恒经过椭圆C:
(t为参数)恒经过椭圆C: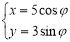 (?为参数)的右焦点F.
(?为参数)的右焦点F.
(Ⅰ)求m的值;
(Ⅱ)设直线l与椭圆C交于A,B两点,求|FA|·|FB|的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源:2015届河南省名校高三上学期期中理科数学试卷(解析版) 题型:选择题
已知定义的R上的函数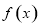 满足
满足 且在
且在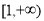 上是增函数,不等式
上是增函数,不等式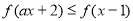 对任意
对任意 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )
A.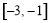 B.
B. C.
C. D.
D.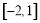
查看答案和解析>>
科目:高中数学 来源:2015届河南省名校高三上学期期中文科数学试卷(解析版) 题型:选择题
已知函数 若
若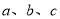 互不相等,且
互不相等,且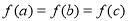 ,则
,则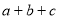 的取值范围是( )
的取值范围是( )
A.(1,2014) B.(1,2015) C.(2,2015) D.[2,2015]
查看答案和解析>>
科目:高中数学 来源:2015届河南省八校高三上学期第一次联考文科数学试卷(解析版) 题型:解答题
抛掷一枚质地不均匀的骰子,出现向上点数为1,2,3,4, 5, 6的概率依次记为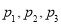 ,
,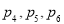 ,经统计发现,数列
,经统计发现,数列 恰好构成等差数列,且
恰好构成等差数列,且 是
是 的3倍.
的3倍.
(Ⅰ)求数列 的通项供式;
的通项供式;
(Ⅱ)甲、乙两人用这枚骰子玩游戏,并规定:掷一次骰子后,若向上点数为奇数,则甲获胜,否者乙获胜,请问这样的规则对甲、乙二人是否公平,请说明理由;
(Ⅲ)甲、乙丙三人用这枚骰子玩游戏,根据掷一次后向上的点数决定胜出者,并制定了公平的游戏方案,试在下面的表格中列举出两种可能的方案(不必证明)
方案序号 | 甲胜出对应点数 | 乙胜出对应点数 | 丙胜出对应点数 |
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com