科目：高中数学 来源： 题型：
某公司生产甲、乙两种桶装产品。已知生产甲产品1桶需耗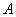
原料1千克、
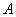原料2千克；生产乙产品1桶需耗原料2千克，原料1千克。每桶甲产品的利润是300元，每桶乙产品的利润是400元。公司在生产这两种产品的计划中，要求每天消耗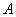、原料都不超过12千克。该公司应如何通过合理安排生产计划，才能使公司获得最大的利润，最大利润是多少元？
查看答案和解析>>
科目：高中数学 来源： 题型：
某旅行社租用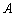
、
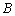两种型号的客车安排900名客人旅行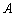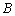，、两种车辆的载客量分别为36人和60人，租金分别为1600元/辆和2400元/辆，旅行社要求租车总数不超过21辆，且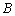型车不多于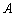型车7辆．求旅行社用于租车的最少租金？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，求
的最小值
，∴
，∴
，
，即
时，
取得最小值
．
的最值情况（ ）
，无最小值 B。有最小值
，无最小值
的不等式
(
)
,则
的取值范围是（ ）
B．
C．
D．
B.
C.
D.
(其中常数
),
是奇函数.
的表达式;
的单调性，并求
，讨函数
的单调性