
(14分)已知函数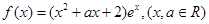 .
.
(Ⅰ)当a=0时,求函数f(x)的图像在点A(1,f(1))处的切线方程;
(Ⅱ)若f(x)在R上单调,求a的取值范围;
(Ⅲ)当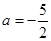 时,求函数f(x)的极小值。
时,求函数f(x)的极小值。
(1)5ex-y-2e=0(2)[-2,2](3)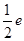
【解析】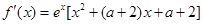
(Ⅰ)当a=0时,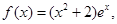
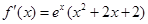 ,………………2分
,………………2分
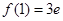 ,
,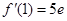 ,
,
∴函数f(x)的图像在点A(1,f(1))处的切线方程为y-3e=5e(x-1),
即5ex-y-2e=0 …………………………………………………………4分
(Ⅱ)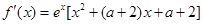 ,
,
考虑到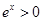 恒成立且
恒成立且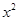 系数为正,
系数为正,
∴f(x)在R上单调等价于 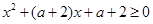 恒成立.
恒成立.
∴(a+2)2-4(a+2)£0,
∴-2£a£2 , 即a 的取值范围是[-2,2],……………………8分
(若得a的取值范围是(-2,2),可扣1分)
(Ⅲ)当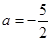 时,
时, 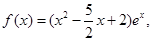
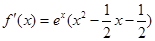 ,
,
………………………………………………………………10分
令 ,得
,得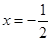 ,或x=1,
,或x=1,
令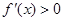 ,得
,得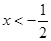 ,或x>1,
,或x>1,
令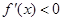 ,得
,得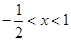 .
………………………………12分
.
………………………………12分
x,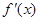 ,f(x)的变化情况如下表
,f(x)的变化情况如下表
|
X |
|
|
|
1 |
|
|
|
+ |
0 |
- |
0 |
+ |
|
f(x) |
|
极大值 |
|
极小值 |
|
所以,函数f(x)的极小值为f(1)=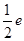 ……………………………………14分
……………………………………14分


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com