
【题目】如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.
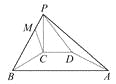
求证:(1)CM∥平面PAD.
(2)平面PAB⊥平面PAD.
【答案】见解析
【解析】
建立空间直角坐标系.(1)可证明![]() 与平面PAD的法向量垂直;也可将
与平面PAD的法向量垂直;也可将![]() 分解为平面PAD内的两个向量的线性组合,利用共面向量定理证明.
分解为平面PAD内的两个向量的线性组合,利用共面向量定理证明.
(2)取AP中点E,利用向量证明BE⊥平面PAD即可.
【证明】由题意可知:
以C为坐标原点,CB所在直线为x轴,CD所在直线为y轴,CP所在直线为z轴建立如图所示的空间直角坐标系Cxyz.
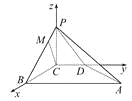
∵PC⊥平面ABCD,
∴∠PBC为PB与平面ABCD所成的角,
∴∠PBC=30°.
∵PC=2,∴BC=2![]() ,PB=4.
,PB=4.
∴D(0,1,0),B(2![]() ,0,0),
,0,0),
A(2![]() ,4,0),P(0,0,2),M(
,4,0),P(0,0,2),M(![]() ,0,),
,0,),
∴![]() =(0,-1,2),
=(0,-1,2),![]() =(2
=(2![]() ,3,0),
,3,0),
![]() =(
=(![]() ,0,).
,0,).
(1)方法一:令n=(x,y,z)为平面PAD的一个法向量,则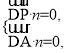
即![]() ∴
∴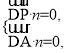
令y=2,得n=(-![]() ,2,1).
,2,1).
∵n·![]() =-
=-![]() ×
×![]() +2×0+1×=0,
+2×0+1×=0,
∴n⊥![]() .又CM平面PAD,
.又CM平面PAD,
∴CM∥平面PAD.
方法二:∵![]() =(0,1,-2),
=(0,1,-2),![]() =(2
=(2![]() ,4,-2),
,4,-2),
假设![]() ∥平面PAD,
∥平面PAD,
则存在x0,y0使![]() =x0
=x0![]() +y0
+y0![]() ,则
,则
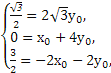 方程组的解为
方程组的解为![]()
∴![]() =-
=-![]() +
+![]() .
.
由共面向量定理知![]() 与
与![]() ,
,![]() 共面,故假设成立.
共面,故假设成立.
又∵CM平面PAD,
∴CM∥平面PAD.
(2)取AP的中点E,连接BE,则E(![]() ,2,1),
,2,1),
![]() =(-
=(-![]() ,2,1).
,2,1).
易知PB=AB,∴BE⊥PA.
又∵![]() ·
·![]() =(-
=(-![]() ,2,1)·(2
,2,1)·(2![]() ,3,0)=0,
,3,0)=0,
∴![]() ⊥
⊥![]() ,∴BE⊥DA.又PA∩DA=A,
,∴BE⊥DA.又PA∩DA=A,
∴BE⊥平面PAD.
又∵BE平面PAB,
∴平面PAB⊥平面PAD.


科目:高中数学 来源: 题型:
【题目】已知真命题:“函数![]() 的图象关于点
的图象关于点![]() 成中心对称图形”的等价条件为“函数
成中心对称图形”的等价条件为“函数![]() 是奇函数”.
是奇函数”.
(1)将函数![]() 的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数
的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数![]() 图象对称中心的坐标;
图象对称中心的坐标;
(2)已知命题:“函数![]() 的图象关于某直线成轴对称图象”的等价条件为“存在实数a和b,使得函数
的图象关于某直线成轴对称图象”的等价条件为“存在实数a和b,使得函数![]() 是偶函数”.断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
是偶函数”.断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点的动直线l与圆![]() 相交于不同的两点A,B.
相交于不同的两点A,B.
(1)求线段AB的中点M的轨迹C的方程;
(2)是否存在实数k,使得直线L:y=k(x﹣4)与曲线C只有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+1,g(x)=4x+1,的定义域都是集合A,函数f(x)和g(x)的值域分别为S和T,
(1)若A=[1,2],求S∩T
(2)若A=[0,m]且S=T,求实数m的值
(3)若对于集合A的任意一个数x的值都有f(x)=g(x),求集合A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有![]() 个人聚会,已知:
个人聚会,已知:
(1)每个人至少同其中![]() 个人互相认识;
个人互相认识;
(2)对于其中任意![]() 个人,或者其中有2人相识,或者余下的人中有2人相识,证明:这
个人,或者其中有2人相识,或者余下的人中有2人相识,证明:这![]() 个人中必有3人两两相识.
个人中必有3人两两相识.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com