
【题目】有![]() 个人聚会,已知:
个人聚会,已知:
(1)每个人至少同其中![]() 个人互相认识;
个人互相认识;
(2)对于其中任意![]() 个人,或者其中有2人相识,或者余下的人中有2人相识,证明:这
个人,或者其中有2人相识,或者余下的人中有2人相识,证明:这![]() 个人中必有3人两两相识.
个人中必有3人两两相识.
【答案】见解析
【解析】
假设这![]() 个人中无3人彼此相识.
个人中无3人彼此相识.
设![]() ,
,![]() 是这
是这![]() 个人中相识的2人,由反证假设可推出余下的
个人中相识的2人,由反证假设可推出余下的![]() 个人中,无1人与
个人中,无1人与![]() ,
,![]() 皆相识.因此,至少有
皆相识.因此,至少有![]() 个不同的人,其中每个人或同
个不同的人,其中每个人或同![]() 相识,或同
相识,或同![]() 相识.
相识.
当![]() 为偶数时,由上述讨论可知,这
为偶数时,由上述讨论可知,这![]() 个人中恰有一半人与
个人中恰有一半人与![]() 相识,而另一半人则与
相识,而另一半人则与![]() 相识.于是,由题设可推出在某一半人中必含2个相识的人.这与反证假设矛盾.
相识.于是,由题设可推出在某一半人中必含2个相识的人.这与反证假设矛盾.
当![]() 为奇数时,
为奇数时,![]() .若这几个人中每人与
.若这几个人中每人与![]() 或
或![]() 相识,则与上述讨论类似,可推出矛盾.
相识,则与上述讨论类似,可推出矛盾.
不然,存在![]() ,他同
,他同![]() ,
,![]() 皆不相识,于是,
皆不相识,于是,![]() 个人中除
个人中除![]() 之外的
之外的![]() 个人中必有一半与
个人中必有一半与![]() 相识,另一半与
相识,另一半与![]() 相识.所有
相识.所有![]() 相识的人互不相识,所有与
相识的人互不相识,所有与![]() 相识的人也互不相识.
相识的人也互不相识.
假设有![]() 个人同
个人同![]() ,
,![]() 皆相识,
皆相识,![]() 个人同
个人同![]() ,
,![]() 皆相识,不难由题设推出
皆相识,不难由题设推出![]() ,并且这
,并且这![]() 个人构成与
个人构成与![]() 相识的人的全部.因而,
相识的人的全部.因而,![]() .不妨设
.不妨设![]() ,由
,由![]() 可知
可知![]() .
.
设![]() 同
同![]() ,
,![]() 皆相识,
皆相识,![]() 与
与![]() 同
同![]() ,
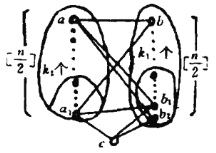
,![]() 皆相识(如图),由于
皆相识(如图),由于![]() 个人中同
个人中同![]() 相识的人至少为
相识的人至少为![]() 个,他们中除
个,他们中除![]() 外同
外同![]() 都相识,故
都相识,故![]() 必与
必与![]() ,
,![]() 之一相识.不妨设
之一相识.不妨设![]() 与
与![]() 相识,则
相识,则![]() ,
,![]() 与
与![]() 是彼此相识的人,此与反证假设相矛盾.因此命题为真.
是彼此相识的人,此与反证假设相矛盾.因此命题为真.


科目:高中数学 来源: 题型:
【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:![]() ,并整理得到频率分布直方图(如图所示).
,并整理得到频率分布直方图(如图所示).
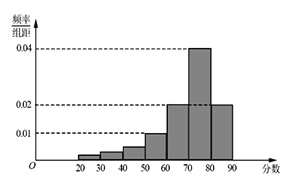
(Ⅰ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间![]() 内的人数.
内的人数.
(Ⅱ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.
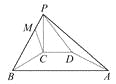
求证:(1)CM∥平面PAD.
(2)平面PAB⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且经过点P
,且经过点P![]() ,过它的左、右焦点
,过它的左、右焦点![]() 分别作直线l1和12.l1交椭圆于A.两点,l2交椭圆于C,D两点, 且
分别作直线l1和12.l1交椭圆于A.两点,l2交椭圆于C,D两点, 且![]()
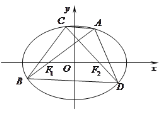
(1)求椭圆的标准方程.
(2)求四边形ACBD的面积S的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 定义域为
定义域为![]() ,且对任意实数
,且对任意实数![]() ,有
,有![]() ,则称
,则称![]() 为“
为“![]() 形函数”,若函数
形函数”,若函数![]() 定义域为
定义域为![]() ,函数
,函数![]() 对任意
对任意![]() 恒成立,且对任意实数
恒成立,且对任意实数![]() ,有
,有![]() ,则称为“对数
,则称为“对数![]() 形函数” .
形函数” .
(1)试判断函数![]() 是否为“
是否为“![]() 形函数”,并说明理由;
形函数”,并说明理由;
(2)若![]() 是“对数
是“对数![]() 形函数”,求实数
形函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 是“
是“![]() 形函数”,且满足对任意
形函数”,且满足对任意![]() ,有
,有![]() ,问
,问![]() 是否为“对数
是否为“对数![]() 形函数”?证明你的结论.
形函数”?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】游乐场的摩天轮匀速旋转,其中心O距地面40.5m,半径40m.若从最低点处登上座天轮,那么人与地面的距离将随时间变化,5min后达到最高点,在你登上摩天轮时开始计时,
(1)求出人与地面距离y与时间t的函数解析式;
(2)从登上摩天轮到旋转一周过程中,有多长时间人与地面距离大于20.5m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() (
(![]() )依次为函数
)依次为函数![]() 图像上的点,点列
图像上的点,点列![]() 、
、![]() 、
、![]() 、
、![]() (
(![]() )依次为
)依次为![]() 轴正半轴上的点,其中
轴正半轴上的点,其中![]() (
(![]() ),对于任意
),对于任意![]() ,点
,点![]() 、
、![]() 、
、![]() 构成一个顶角的顶点为
构成一个顶角的顶点为![]() 的等腰三角形.
的等腰三角形.
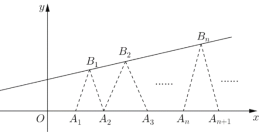
(1)证明:数列![]() 是等差数列;
是等差数列;
(2)证明:![]() 为常数,并求出数列
为常数,并求出数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)在上述等腰三角形![]() 中,是否存在直角三角形?若存在,求出
中,是否存在直角三角形?若存在,求出![]() 值,若不存在,请说明理由.
值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).以原点
).以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)若直线![]() 与圆
与圆![]() 有公共点,试求实数
有公共点,试求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,过点
时,过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交圆
交圆![]() 于
于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com