
【题目】已知函数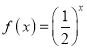 与
与![]() ,若对任意的
,若对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,则实数
,则实数![]() 的取值范围是______.
的取值范围是______.
【答案】![]()
【解析】
求出函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,由题意可知,由
,由题意可知,由![]() ,可得出
,可得出![]() ,由题意知,函数
,由题意知,函数![]() 在区间
在区间![]() 上的值域包含
上的值域包含![]() ,然后对
,然后对![]() 分
分![]() 、
、![]() 、
、![]() 三种情况分类讨论,求出函数
三种情况分类讨论,求出函数![]() 在区间
在区间![]() 上的值域,可得出关于实数
上的值域,可得出关于实数![]() 的不等式(组),解出即可.
的不等式(组),解出即可.
由于函数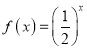 在
在![]() 上的减函数,则
上的减函数,则![]() ,即
,即![]() ,
,
所以,函数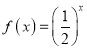 在区间
在区间![]() 上的值域为
上的值域为![]() .
.
对于函数![]() ,内层函数为
,内层函数为![]() ,外层函数为
,外层函数为![]() .
.
令![]() ,得
,得![]() .
.
由题意可知,函数![]() 在区间
在区间![]() 上的值域包含
上的值域包含![]() .
.
函数![]() 的图象开口向上,对称轴为直线
的图象开口向上,对称轴为直线![]() .
.
(i)当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,则
上单调递增,则![]() ,
,![]() ,即
,即![]() ,
,
此时,函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,
,
由题意可得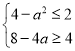 ,解得
,解得![]() ,此时,
,此时,![]() ;
;
(ii)当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,则
上单调递增,则![]() ,
,![]() ,即
,即![]() ,
,
此时,函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,
,
由题意可得![]() ,解得
,解得![]() 或
或![]() ,此时
,此时![]() ;
;
(iii)当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,则
上单调递减,则![]() ,
,![]() ,则函数
,则函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,
,
由题意可得![]() ,解得
,解得![]() ,此时,
,此时,![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知真命题:“函数![]() 的图象关于点
的图象关于点![]() 成中心对称图形”的等价条件为“函数
成中心对称图形”的等价条件为“函数![]() 是奇函数”.
是奇函数”.
(1)将函数![]() 的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数
的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数![]() 图象对称中心的坐标;
图象对称中心的坐标;
(2)已知命题:“函数![]() 的图象关于某直线成轴对称图象”的等价条件为“存在实数a和b,使得函数
的图象关于某直线成轴对称图象”的等价条件为“存在实数a和b,使得函数![]() 是偶函数”.断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
是偶函数”.断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体![]() 中,
中,![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() .
.
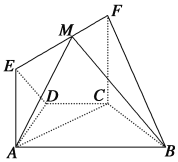
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,设平面
上运动,设平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张军在网上经营了一家干果店,销售的干果中有松子、开心果、腰果、核桃,价格依次为120元/千克、80元/千克、70元/千克、40元/千克.为了增加销量,张军对以上四种干果进行促销,若一次性购买干果的总价达到150元,顾客就少付x(x∈Z)元,每笔订单顾客在网上支付成功后,张军会得到支付款的80%.
①当x=15时,顾客一次性购买松子和腰果各1千克,需要支付_________________元;
②在促销活动中,为保证张军每笔订单得到的金额均不低于促销的总价的70%,则x的最大值为___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有![]() 个人聚会,已知:
个人聚会,已知:
(1)每个人至少同其中![]() 个人互相认识;
个人互相认识;
(2)对于其中任意![]() 个人,或者其中有2人相识,或者余下的人中有2人相识,证明:这
个人,或者其中有2人相识,或者余下的人中有2人相识,证明:这![]() 个人中必有3人两两相识.
个人中必有3人两两相识.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com