练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．i为虚数单位，若$\frac{a}{1-i}$=$\frac{1+i}{i}$，则a的值为-2i．

    分析 利用复数的运算法则、复数相等即可得出．

    解答 解：由已知$\frac{a}{1-i}$=$\frac{1+i}{i}$得，ai=（1-i）（1+i）=2，a=$\frac{2}{i}$=-2i．
    故答案为：-2i．

    点评 本题考查了复数的运算法则、复数相等，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．在△ABC中，A（3，2），B（-1，5），点C在直线y=3x+3上，若△ABC的面积为10，求点C的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知数列{an}，a1=1，满足${a_{n+1}}-2{a_n}={2^n}$．
    （1）求证：数列$\{\frac{a_n}{2^n}\}$是等差数列，并求数列{an}的通项公式；
    （2）若数列{bn}满足b1+2b2+…+nbn=an，对一切n∈N*都成立，求数列{bn}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．由约束条件$\left\{\begin{array}{l}x，y≥0\\ y≤-3x+3\\ y≤kx+1\end{array}\right.$，确定的可行域D能被半径为$\frac{{\sqrt{2}}}{2}$的圆面完全覆盖，则实数k的取值范围是$（-∞，\frac{1}{3}]$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知f（x）=$\frac{x}{{e}^{x}}$+xex，定义a1（x）=f'（x），a2（x）=[a1（x）]′，…，an+1（x）=[an（x）]′，n∈N*．经计算令a1（x）=$\frac{1-x}{e^x}+（{x+1}）{e^x}，{a_2}（x）=\frac{x-2}{e^x}+（{x+2}）{e^x}，{a_3}（x）=\frac{3-x}{e^x}+（{x+3}）{e^x}$，…，令g（x）=a2017（x），则g（1）=2018e+$\frac{2016}{e}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知f（x）=2+acos x（a≠0）．
    （1）判断函数的奇偶性；
    （2）求函数的单调区间；
    （3）求函数的最小正周期．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知数列{an}的通项公式an=4n-20，则如图算法的输出结果是（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．某种新产品投放市场一段时间后，经过调研获得了时间x（天数）与销售单价y（元）的一组数据，且做了一定的数据处理（如表），并作出了散点图（如图）．
    $\overline{x}$$\overline{y}$$\overline{w}$$\sum_{i=1}^{10}（{x}_{i}-\overline{x}）^{2}$$\sum_{i=1}^{10}（{w}_{i}-\overline{w}）^{2}$$\sum_{i=1}^{10}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）$$\sum_{i=1}^{10}（{w}_{i}-\overline{w}）（{y}_{i}-\overline{y}）$
    1.6337.80.895.150.92-20.618.40
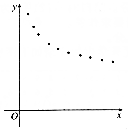    表中wi=$\frac{1}{{x}_{i}}$，$\overline{w}$=$\frac{1}{10}$$\sum_{i=1}^{10}{w}_{i}$．
    （Ⅰ）根据散点图判断，$\widehat{y}$=$\widehat{a}$+$\widehat{b}$x与$\widehat{y}$=$\widehat{c}$+$\frac{\widehat{d}}{x}$哪一个更适宜作价格y关于时间x的回归方程类型？（不必说明理由）
    （Ⅱ）根据判断结果和表中数据，建立y关于x的回归方程；
    （Ⅲ）若该产品的日销售量g（x）（件）与时间x的函数关系为g（x）=$\frac{-100}{x}$+120（x∈N*），求该产品投放市场第几天的销售额最高？最高为多少元？
    附：对于一组数据（u1，v1），（u2，v2），（u3，v3），…，（un，vn），其回归直线v=α+βu的斜率和截距的最小二乘估计分别为$\widehat{β}$=$\frac{\sum_{i=1}^{n}（{v}_{i}-\overline{v}）（{u}_{i}-\overline{u}）}{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）^{2}}$，$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．将函数f（x）=2$\sqrt{3}$cos2x-2sinxcosx-$\sqrt{3}$的图象向左平移t（t＞0）个单位，所得图象对应的函数为奇函数，则t的最小值为（　　）
    A．$\frac{2π}{3}$B．$\frac{π}{3}$C．$\frac{π}{2}$D．$\frac{π}{6}$

    查看答案和解析>>

    同步练习册答案