已知函数f(x)=2x-a(a∈N*、x∈R),数列an满足a1=-a,an+1-an=f(n).
(1)求数列an的通项公式;
(2)当a5与a6这两项中至少有一项为an中的最小项时,求a的值;
(3)若数列bn满足对?n∈N*,都有b1+2b2+22b3+…+2n-1bn=an+1成立,求数列{bn}中的最大项.
解:(1)a
n=(a
n-a
n-1)+(a
n-1-a
n-2)++(a
2-a
1)+a
1=f(n-1)+f(n-2)+…+f(1)-a=n(n-1-a).
(2)a
n=n
2-(1+a)n是关于n的二次函数,二次项系数为1(>0),
所以“a
5与a
6这两项中至少有一项为a
n中的最小项”当且仅当
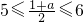
,9≤a≤11,a=9、10、11.
(3)由b
1+2b
2+2
2b
3++2
n-1b
n=a
n+1得2
n-1b
n=a
n+1-a
n=f(n)=2n-a,从而b
n=2
1-n(2n-a),解
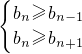
即
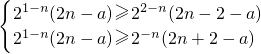
得
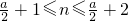
若a=2k(k∈N
*)是偶数,则最小项为b
k+1=b
k+2=2
1-k;
若a=2k-1(k∈N
*)是奇数,则最小项为b
k+1=3×2
-k.
分析:(1)a
n=(a
n-a
n-1)+(a
n-1-a
n-2)+…+(a
2-a
1)+a
1=f(n-1)+f(n-2)+…+f(1)-a,由此能求出它的通项公式.
(2)a
n=n
2-(1+a)n是关于n的二次函数,二次项系数为1(>0),所以“a
5与a
6这两项中至少有一项为a
n中的最小项”当且仅当
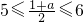
,9≤a≤11,由此能求出a的值.
(3)由b
1+2b
2+2
2b
3++2
n-1b
n=a
n+1得2
n-1b
n=a
n+1-a
n=f(n)=2n-a,从而b
n=2
1-n(2n-a),由此分别讨论,能求出数列{b
n}中的最大项.
点评:(1)是用叠加与等差数列性质求通项;(2)是函数角度看数列,并用二次函数性质求解数列问题;(3)是从“和式”中分离数列,用比较法讨论数列的最大项.

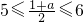 ,9≤a≤11,a=9、10、11.
,9≤a≤11,a=9、10、11.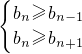
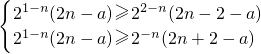 得
得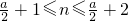
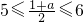 ,9≤a≤11,由此能求出a的值.
,9≤a≤11,由此能求出a的值.
