(1)证明:由题设an+1=(1+q)an-qan-1(n≥2),得an+1-an=q(an-an-1),
即bn=qbn-1,n≥2.
又b1=a2-a1=1,q≠0,所以{bn}是首项为1,公比为q的等比数列.
(2)解:由(1),a2-a1=1,a3-a2=q,…
an-an-1=qn-2(n≥2).
将以上各式相加,得an-a1=1+q+…+qn-2(n≥2).
所以当n≥2时,an=
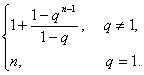
上式对n=1显然成立.
(3)解:由(2),当q=1时,显然a3不是a6与a9的等差中项,故q≠1.
由a3-a6=a9-a3可得q5-q2=q2-q8,
由q≠0q3-1="1-q6, " ①
整理得(q3)2+q3-2=0,
解得q3=-2或q3=1(舍去).
于是q=
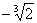
.
另一方面,an-an+3=
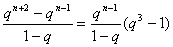
,
an+6-an=
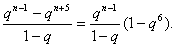
由①可得an-an+3=an+6-an,n∈N*.
所以对任意的n∈N*,an是an+3与an+6的等差中项.

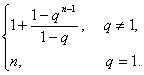
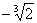 .
.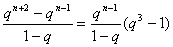 ,
,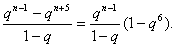


 名校课堂系列答案
名校课堂系列答案 的递推公式
的递推公式 [
[