
| ||||
|
| X | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
| 1 |
| 210 |
| 209 |
| 210 |


科目:高中数学 来源: 题型:
| 分组 | 频数 | 频率 |
| [45,60) | 2 | 0.04 |
| [60,75) | 4 | 0.08 |
| [75,90) | 8 | 0.16 |
| [90,105) | 11 | 0.22 |
| [105,120) | 15 | 0.30 |
| [120,135) | a | b |
| [135,150] | 4 | 0.08 |
| 合计 | 50 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:江西省宜春市2012届高三模拟考试数学理科试题 题型:044
为丰富高三学生的课余生活,提升班级的凝聚力,某校高三年级6个班(含甲、乙)举行唱歌比赛.比赛通过随机抽签方式决定出场顺序.
求:(1)甲、乙两班恰好在前两位出场的概率;
(2)比赛中甲、乙两班之间的班级数记为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省高三最后一次综合测试数学试卷(解析版) 题型:解答题
为丰富高三学生的课余生活,提升班级的凝聚力,某校高三年级6个班(含甲、乙)举行唱歌比赛.比赛通过随机抽签方式决定出场顺序.
求:(1)甲、乙两班恰好在前两位出场的概率;
(2)比赛中甲、乙两班之间的班级数记为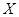 ,求
,求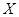 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省宜春市高三模拟考试理科数学试卷(解析版) 题型:解答题
(本小题12分)为丰富高三学生的课余生活,提升班级的凝聚力,某校高三年级6个班(含甲、乙)举行唱歌比赛.比赛通过随机抽签方式决定出场顺序.
求:(1)甲、乙两班恰好在前两位出场的概率;
(2)比赛中甲、乙两班之间的班级数记为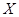 ,求
,求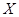 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com