
【题目】已知函数![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 有极小值,求该极小值的取值范围.
有极小值,求该极小值的取值范围.
【答案】(Ⅰ):当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;当
;当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(Ⅱ)![]()
【解析】试题分析:(1)对函数求导得到导函数,根据导函数的正负求得函数的单调性;(2)结合第一问得到当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,所以
,所以![]() ,对此表达式进行求导,研究单调性,求最值即可.
,对此表达式进行求导,研究单调性,求最值即可.
详解:
(Ⅰ)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 内单调递增,
内单调递增,
②当![]() 时,令
时,令![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
综上所述:当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(Ⅱ)①当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 内单调递增,没有极值;
内单调递增,没有极值;
②当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,
所以![]() ,
,
记![]() ,则
,则![]() ,由
,由![]() 得
得![]() ,
,
所以![]() ,
,
所以函数![]() 的极小值的取值范围是
的极小值的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】给出如下四个命题:①若“![]() 且
且![]() ”为假命题,则
”为假命题,则![]() 均为假命题;②命题“若
均为假命题;②命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”; ③“
”; ③“![]() ,则
,则![]() ”的否定是“
”的否定是“![]() ,则
,则![]() ”;④在
”;④在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充要条件.其中正确的命题的个数是( )
”的充要条件.其中正确的命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接中国共产党的十九大的到来,某校举办了“祖国,你好”的诗歌朗诵比赛.该校高三年级准备从包括甲、乙、丙在内的7名学生中选派4名学生参加,要求甲、乙、丙这3名同学中至少有1人参加,且当这3名同学都参加时,甲和乙的朗诵顺序不能相邻,那么选派的4名学生不同的朗诵顺序的种数为( )
A. 720 B. 768 C. 810 D. 816
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.右图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图.已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群” .
(1)求m,n的值,并求这100名学生月消费金额的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)根据已知条件完成下面2×2列联表,并判断能否有90%的把握认为“高消费群”与性别有关?
高消费群 | 非高消费群 | 合计 | |
男 | |||
女 | 10 | 50 | |
合计 |
(参考公式:![]() ,其中
,其中![]() )
)
P( | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() ,
,![]() 是椭圆与
是椭圆与![]() 轴的两个交点,
轴的两个交点,![]() 为椭圆C的上顶点,设直线
为椭圆C的上顶点,设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)设直线![]() 与轴交于点
与轴交于点![]() ,交椭圆于
,交椭圆于![]() 、
、![]() 两点,且满足
两点,且满足![]() ,当
,当![]() 的面积最大时,求椭圆
的面积最大时,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一辆赛车在一个周长为![]() 的封闭跑道上行驶,跑道由几段直道和弯道组成,图
的封闭跑道上行驶,跑道由几段直道和弯道组成,图![]() 反映了赛车在“计时赛”整个第二圈的行驶速度与行驶路程之间的关系.
反映了赛车在“计时赛”整个第二圈的行驶速度与行驶路程之间的关系.
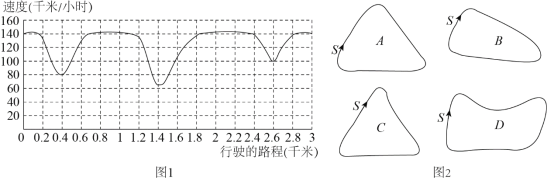
根据图1,有以下四个说法:
①在这第二圈的![]() 到
到![]() 之间,赛车速度逐渐增加;
之间,赛车速度逐渐增加;
②在整个跑道中,最长的直线路程不超过![]() ;
;
③大约在这第二圈的![]() 到
到![]() 之间,赛车开始了那段最长直线路程的行驶;
之间,赛车开始了那段最长直线路程的行驶;
④在图![]() 的四条曲线(
的四条曲线(![]() 为初始记录数据位置)中,曲线
为初始记录数据位置)中,曲线![]() 最能符合赛车的运动轨迹.
最能符合赛车的运动轨迹.
其中,所有正确说法的序号是__________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一鲜花店一个月(30天)某种鲜花的日销售量与销售天数统计如下:
日销售量(枝) | 0~49 | 50~99 | 100~149 | 150~199 | 200~250 |
销售天数(天) | 3天 | 3天 | 15天 | 6天 | 3天 |
将日销售量落入各组区间的频率视为概率.
(1)试求这30天中日销售量低于100枝的概率;
(2)若此花店在日销售量低于100枝的6天中选择2天作促销活动,求这2天的日销售量都低于50枝的概率(不需要枚举基本事件).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com