
【题目】如图,在三棱锥A-BCD中,AB=a,AC=AD=b,BC=CD=DB=c(a>0,b>0,c>0)该三棱锥的截面EFGH平行于AB、CD,分别交AD、AC、BC、BD于E、F、G、H.

(1)证明:AB⊥CD;
(2)求截面四边形EFGH面积的最大值,并说明面积取最大值时截面的位置.
【答案】(1)详见解析(2)截面为中截面时,截面四边形EFGH面积的最大为![]() ,
,
【解析】
(1)要证AB⊥CD,需证CD⊥平面ABI,需证AI⊥CD,BI⊥CD,由已知可证;
(2)先证EFGH是矩形,再表示出SEFGH=k(1﹣k)ac=﹣ac(k![]() )2
)2![]() ,可求最值.
,可求最值.
(1)取CD中点I,连结AI、BI,
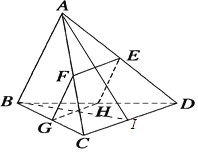
∵AC=AD,∴AI⊥CD,
∵BC=BD,∴BI⊥CD,
又AI∩BI=I,∴CD⊥平面ABI,
又ABABI,∴AB⊥CD;
(2)∵AB∥平面EFGH,AB平面ABC,
平面EFGH∩平面ABC=FG,∴AB∥FG,
同理可证AB∥EH,∴FG∥EH,
同理可证EF∥HG,
∴EFGH是平行四边形,
由(1)AB⊥CD知EF⊥EH,
∴EFGH是矩形,
设GF=ka,则GH=(1﹣k)c,
SEFGH=k(1﹣k)ac=﹣ac(k![]() )2
)2![]() ,
,
当k![]() 时,截面四边形EFGH面积的最大为
时,截面四边形EFGH面积的最大为![]() ,
,
此时,截面为中截面.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在对人们的休闲方式的一次调查中,用简单随机抽样方法调查了125人,其中女性70人,男性55人.女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外35人主要的休闲方式是运动.
(1)根据以上数据建立一个![]() 列联表;
列联表;
(2)能否在犯错误的概率不超过0.025的前提下,认为性别与休闲方式有关系?
(3)在休闲方式为看电视的人中按分层抽样方法抽取6人参加某机构组织的健康讲座,讲座结束后再从这6人中抽取2人作反馈交流,求参加交流的恰好为2位女性的概率.
附:
P( | 0.05 | 0.025 | 0.010 |
k | 3.841 | 5.024 | 6.635 |
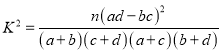
休闲方式 性别 | 看电视 | 运动 | 合计 |
女 | |||
男 | |||
合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设正项数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足:
,且满足:![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若正项等比数列![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意
,若对任意![]() ,均有
,均有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产开发商投资81万元建一座写字楼,第一年装修维护费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元.
(1)若扣除投资和各种装修维护费,则从第几年开始获取纯利润?
(2)若干年后开发商为了投资其他项目,有两种处理方案:①纯利润总和最大时,以10万元出售该楼;②年平均利润最大时以46万元出售该楼,问哪种方案更优?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有如下命题:
有如下命题:
①![]() ; ②函数的图象关于原点中心对称;
; ②函数的图象关于原点中心对称;
③函数的定义域与值域相同; ④函数的图象必经过第二、四象限.
其中正确命题的个数是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2ex+3x2-2x+1+b,x∈R的图象在x=0处的切线方程为y=ax+2.
(1)求函数f(x)的单调区间与极值;
(2)若存在实数x,使得f(x)-2x2-3x-2-2k≤0成立,求整数k的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com