
已知二次函数 ,满足
,满足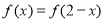 ,且方程
,且方程 有两个相等的实根.
有两个相等的实根.
(1)求函数 的解析式;
的解析式;
(2)当
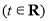 时,求函数
时,求函数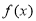 的最小值
的最小值 的表达式.
的表达式.
(1)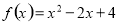 ;(2)
;(2)
【解析】
试题分析:(1)通过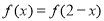 ,求出函数的对称轴方程,求出二次函数的对称轴方程,即可求b,利用方程
,求出函数的对称轴方程,求出二次函数的对称轴方程,即可求b,利用方程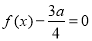 有两个相等的实根,判别式等于0,求出
有两个相等的实根,判别式等于0,求出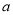 ,即可求解函数
,即可求解函数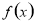 的解析式;
的解析式;
(2)求出函数的对称轴方程,利用对称轴在[t,t+1]内以及区间外,分别求出函数的最小值,即可求函数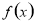 的最小值
的最小值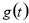 的表达式.
的表达式.
试题解析:(1)由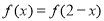 ,可知函数的对称轴方程为
,可知函数的对称轴方程为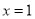 ,而二次函数
,而二次函数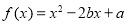 的对称轴是
的对称轴是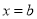 ,所以,对称轴:
,所以,对称轴: ,由方程
,由方程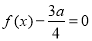 有两个相等的实根可得:
有两个相等的实根可得: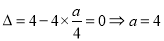 ;∴
;∴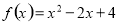 .
.
(2)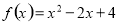
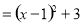 ;
;
①当t+1≤1,即t≤0时,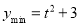 ;
;
②当t<1<t+1,即0<t<1时,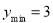 ;
;
③当t≥1时, ;
;
综上:
考点:(1)二次函数在闭区间上的最值;(2)函数解析式的求解及常用方法.


科目:高中数学 来源:2015届福建省高二上学期期末考理科数学试卷(解析版) 题型:解答题
已知函数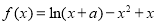 ,
,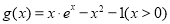 ,且
,且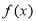 点
点 处取得极值.
处取得极值.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若关于 的方程
的方程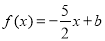 在区间
在区间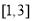 上有解,求
上有解,求 的取值范围;
的取值范围;
(Ⅲ)证明: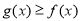 .
.
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末理科数学试卷(解析版) 题型:选择题
在区间(0, 1)内任取两个实数,则这两个实数的和大于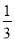 的概率为( )
的概率为( )
A.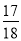 B.
B. C.
C. D.
D.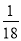
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末理科数学试卷(解析版) 题型:选择题
如图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.从这个茎叶图可以看出甲、乙两名运动员得分的中位数分别是( ).

A.31,26 B.36,23 C.36,26 D.31,23
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末文科数学试卷(解析版) 题型:填空题
设f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x2-x,则f(1)=________.
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末文科数学试卷(解析版) 题型:选择题
若函数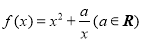 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.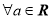 ,
,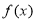 在
在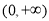 上是增函数
上是增函数
B.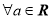 ,
,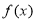 在
在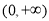 上是减函数
上是减函数
C.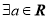 ,
,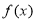 是偶函数
是偶函数
D.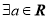 ,
,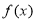 是奇函数
是奇函数
查看答案和解析>>
科目:高中数学 来源:2015届福建省四地六校高二下学期第一次月考文科数学试卷(解析版) 题型:填空题
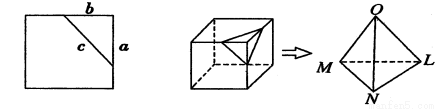
在平面上,我们用一直线去截正方形的一个角,那么截下的一个直角三角形,按如图所标边长,由勾股定理有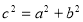 .设想正方形换成正方体,把截线换成如图截面,这时从正方体上截下三条侧棱两两垂直的三棱锥
.设想正方形换成正方体,把截线换成如图截面,这时从正方体上截下三条侧棱两两垂直的三棱锥 ,如果用
,如果用 表示三个侧面面积,
表示三个侧面面积,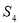 表示截面面积,那么类比得到的结论是 .
表示截面面积,那么类比得到的结论是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com