
已知函数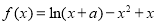 ,
,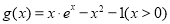 ,且
,且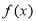 点
点 处取得极值.
处取得极值.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若关于 的方程
的方程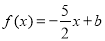 在区间
在区间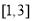 上有解,求
上有解,求 的取值范围;
的取值范围;
(Ⅲ)证明: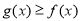 .
.
(1)0;(2)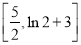 .
.
【解析】
试题分析:利用导数及极值来解决问题时一般问题不会太难,应抓住关键问题由此入手.(2)解决类似的问题时,注意区分函数的最值和极值.求函数的最值时,要先求函数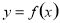 在区间
在区间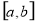 内使
内使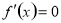 的点,再计算函数
的点,再计算函数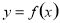 在区间内所有使
在区间内所有使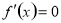 的点和区间端点处的函数值,最后比较即得.(3)分类讨论是学生在学习过程中的难点,要找好临界条件进行讨论.
的点和区间端点处的函数值,最后比较即得.(3)分类讨论是学生在学习过程中的难点,要找好临界条件进行讨论.
试题解析:(Ⅰ)∵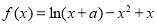 , ∴
, ∴
∵函数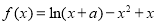 在点
在点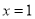 处取得极值,
处取得极值,
∴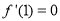 ,即当
,即当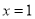 时
时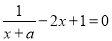 ,
,
∴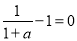 ,则得
,则得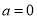 .经检验符合题意
.经检验符合题意
(Ⅱ)∵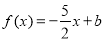 ,∴
,∴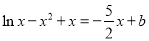 ,
,
∴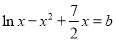 .
.
令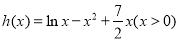 ,
,
则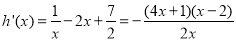 .
.
∴当 时,
时,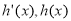 随
随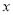 的变化情况表:
的变化情况表:
| 1 | (1,2) | 2 | (2,3) | 3 |
|
| + | 0 | - |
|
|
| ↗ | 极大值 | ↘ |
|
计算得: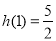 ,
,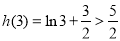 ,
,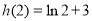 ,
,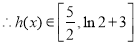
所以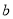 的取值范围为
的取值范围为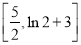 .
.
(Ⅲ)证明:令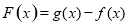
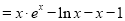
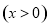 ,
,
则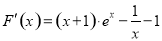
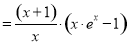 ,
,
令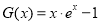 ,则
,则 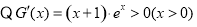 ,
,
 函数
函数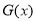 在
在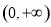 递增,
递增,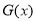 在
在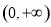 上的零点最多一个
上的零点最多一个
又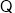
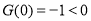 ,
,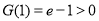 ,
,
 存在唯一的
存在唯一的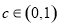 使得
使得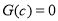 ,
,
且当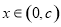 时,
时, ;当
;当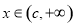 时,
时,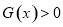 .
.
即当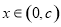 时,
时,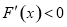 ;当
;当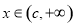 时,
时,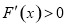 .
.

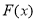 在
在 递减,在
递减,在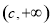 递增,
递增,
从而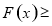
 .
.
由 得
得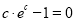 即
即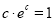 ,两边取对数得:
,两边取对数得: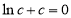 ,
,
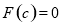 ,
,

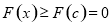 ,
,
从而证得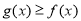 .
.
考点:(1)利用导数极值求参量的取值或范围 ;(2)导数即函数性质的综合运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届福建省高二下学期期中考理科数学试卷(解析版) 题型:选择题
如果对定义在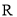 上的函数
上的函数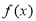 ,对任意两个不相等的实数
,对任意两个不相等的实数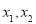 ,都有
,都有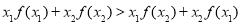 ,则称函数
,则称函数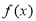 为“
为“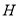 函数”.给出下列函数
函数”.给出下列函数
①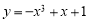 ;②
;②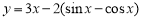 ;③
;③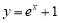 ;④
;④ .以上函数是“
.以上函数是“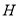 函数”的共有( )
函数”的共有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:填空题
椭圆有这样的光学性质:从椭圆的一个焦点发出的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.今有一个水平放置的椭圆形球盘,点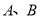 是它的两个焦点,长轴长
是它的两个焦点,长轴长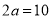 ,焦距
,焦距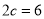 ,静放在点
,静放在点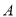 的小球(小球的半径不计)从点
的小球(小球的半径不计)从点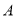 沿直线(不与长轴共线)发出,经椭圆壁反弹后第一次回到点
沿直线(不与长轴共线)发出,经椭圆壁反弹后第一次回到点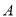 时,小球经过的路程为 .
时,小球经过的路程为 .
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末文科数学试卷(解析版) 题型:解答题
已知二次函数 ,满足
,满足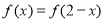 ,且方程
,且方程 有两个相等的实根.
有两个相等的实根.
(1)求函数 的解析式;
的解析式;
(2)当
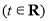 时,求函数
时,求函数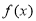 的最小值
的最小值 的表达式.
的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com