
(本题满分16分)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点, =2
=2 =2.
=2.
(1)求证: ;
;
(2)求证: ∥平面
∥平面 ;
;
(3)求三棱锥 的体积
的体积 .
.

解:(1)在Rt△ABC中,AB=1,∠BAC=60°,
∴BC= ,AC=2.取
,AC=2.取 中点
中点 ,连AF, EF,
,连AF, EF,
∵PA=AC=2,∴PC⊥ . ………………………………………………………2分
. ………………………………………………………2分
∵PA⊥平面ABCD, 平面ABCD,
平面ABCD,
∴PA⊥ ,又∠ACD=90°,即
,又∠ACD=90°,即 ,
,
∴ ,∴
,∴ ,
,
∴ . …………………………………………………………………… 4分
. …………………………………………………………………… 4分
∴ .
∴PC⊥
.
∴PC⊥ .…………………………………………………6分
.…………………………………………………6分
(2)证法一:取AD中点M,连EM,CM.则

EM∥PA.∵EM  平面PAB,PA
平面PAB,PA 平面PAB,
平面PAB,
∴EM∥平面PAB. ……………………………………………………………………8分
在Rt△ACD中,∠CAD=60°,AC=AM=2,
∴∠ACM=60°.而∠BAC=60°,∴MC∥AB.
∵MC  平面PAB,AB
平面PAB,AB 平面PAB,
平面PAB,
∴MC∥平面PAB. ……………………………………………………………………10分
∵EM∩MC=M,∴平面EMC∥平面PAB.
∵EC 平面EMC,∴EC∥平面PAB.………………………………………………12分
平面EMC,∴EC∥平面PAB.………………………………………………12分
证法二:延长DC、AB,设它们交于点N,连PN.
∵∠NAC=∠DAC=60°,AC⊥CD,∴C为ND的中点.…………………………8分
∵E为PD中点,∴EC∥PN …………………………………………………………10分
∵EC  平面PAB,PN
平面PAB,PN 平面PAB,∴EC∥平面PAB. ………………… 12分(3)由(1)知AC=2,EF=CD, 且EF⊥平面PAC.
平面PAB,∴EC∥平面PAB. ………………… 12分(3)由(1)知AC=2,EF=CD, 且EF⊥平面PAC.
在Rt△ACD中,AC=2,∠CAD=60°,∴CD=2 ,得EF=.……………14分
,得EF=.……………14分
则V=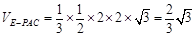 . ………………………………… 16分
. ………………………………… 16分
【解析】略


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
(本题满分16分)
在平面直角坐标系![]() 中,已知圆心在第二象限、半径为
中,已知圆心在第二象限、半径为![]() 的圆
的圆![]() 与直线
与直线![]() 相切于坐标原点
相切于坐标原点![]() .椭圆
.椭圆![]() 与圆
与圆![]() 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)试探究圆![]() 上是否存在异于原点的点
上是否存在异于原点的点![]() ,使
,使![]() 到椭圆右焦点
到椭圆右焦点![]() 的距离等于线段
的距离等于线段![]() 的长.若存在,请求出点
的长.若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)在平面直角坐标系![]() 中,已知圆心在第二象限、半径为
中,已知圆心在第二象限、半径为![]() 的圆
的圆![]() 与直线
与直线![]() 相切于坐标原点
相切于坐标原点![]() .椭圆
.椭圆![]() 与圆
与圆![]() 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为![]() .
.
(1)求圆![]() 的方程;
的方程;
查看答案和解析>>
科目:高中数学 来源:江苏省镇江市09-10学年高二第二学期期末考试数学试题文科 题型:解答题
(本题满分16分)
在区间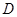 上,如果函数
上,如果函数 为增函数,而函数
为增函数,而函数 为减函数,则称函数
为减函数,则称函数 为“弱增”函数.已知函数
为“弱增”函数.已知函数
(1)判断函数 在区间
在区间 上是否为“弱增”函数
上是否为“弱增”函数
(2)设 ,证明
,证明
(3)当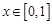 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com