
分析 (Ⅰ)求出直线、圆的普通方程,利用直线l与圆C的相交弦长不小于$\sqrt{2}$,求实数m的取值范围;
(Ⅱ)P(cosα,1+sinα),Q(x,y),则x=$\frac{1}{2}$(cosα+2),y=$\frac{1}{2}$(1+sinα),消去α,整理可得线段PA的中点Q的轨迹方程
解答 解:(Ⅰ)直线l的参数方程为$\left\{\begin{array}{l}{x=t}\\{y=mt}\end{array}\right.$(t为参数),普通方程为y=mx,
圆C的参数方程为$\left\{\begin{array}{l}{x=cosa}\\{y=1+sina}\end{array}\right.$(a为参数),普通方程为x2+(y-1)2=1.
圆心到直线l的距离d=$\frac{1}{\sqrt{{m}^{2}+1}}$,相交弦长=2$\sqrt{1-\frac{1}{{m}^{2}+1}}$,
∴2$\sqrt{1-\frac{1}{{m}^{2}+1}}$≥$\sqrt{2}$,∴m≤-1或m≥1;
(Ⅱ)设P(cosα,1+sinα),Q(x,y),则x=$\frac{1}{2}$(cosα+2),y=$\frac{1}{2}$(1+sinα),
消去α,整理可得线段PA的中点Q的轨迹方程(x-1)2+(y-$\frac{1}{2}$)2=$\frac{1}{4}$.
点评 本题考查参数方程与普通方程的转化,考查直线与圆位置关系的运用,考查轨迹方程,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{4034}{4035}$ | B. | $\frac{2017}{4035}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2017}{2018}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1) | B. | (-2,+∞) | C. | (-∞,-$\frac{3}{2}$)∪(-1,+∞) | D. | (-2,-$\frac{3}{2}$)∪(-$\frac{3}{2}$,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-4y2=1 | B. | $\frac{{x}^{2}}{4}$$-\frac{{y}^{2}}{64}$=1 | C. | $\frac{{y}^{2}}{4}$-x2=1 | D. | y2-4x2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
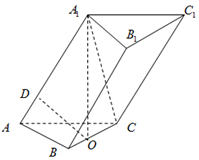 三棱柱ABC-A1B1C1的底面ABC是等边三角形,BC的中点为O,A1O⊥底面ABC,AA1与底面ABC所成的角为$\frac{π}{3}$,点D在棱AA1上,且AD=$\sqrt{3}$,AB=4.
三棱柱ABC-A1B1C1的底面ABC是等边三角形,BC的中点为O,A1O⊥底面ABC,AA1与底面ABC所成的角为$\frac{π}{3}$,点D在棱AA1上,且AD=$\sqrt{3}$,AB=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com