
分析 (1)利用函数是奇函数的定义,列出方程,比较求解n,利用f(2)=$\frac{5}{3}$,求解m即可.
(2)利用函数的单调性的定义判断求解即可.
解答 解:(1)∵f(x)是奇函数,∴f(-x)=-f(x),
∴$\frac{m{x}^{2}+2}{-3x+n}$=-$\frac{mx{\;}^{2}+2}{3x+n}$=$\frac{m{x}^{2}+2}{-3x-n}$.
比较得n=-n,n=0.
又f(2)=$\frac{5}{3}$,∴$\frac{4m+2}{6}$=$\frac{5}{3}$,解得m=2.
即实数m和n的值分别是2和0.
(2)函数f(x)在(-∞,-1]上为增函数,在(-1,0)上为减函数.
证明如下:由(1)可知f(x)=$\frac{2x2+2}{3x}$=$\frac{2x}{3}$+$\frac{2}{3x}$.
设x1<x2<0,
则f(x1)-f(x2)=$\frac{2}{3}$(x1-x2)$\b\lc\(\rc\)(\a\vs4\al\co1(1-\frac{1}{x1x2}))$
=$\frac{2}{3}$(x1-x2)•$\frac{x1x2-1}{x1x2}$.
当x1<x2≤-1时,x1-x2<0,x1x2>0,x1x2-1>0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴函数f(x)在(-∞,-1]上为增函数;
当-1<x1<x2<0时,
x1-x2<0,x1x2>0,x1x2-1<0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴函数f(x)在(-1,0)上为减函数.
点评 本题考查函数的单调性以及函数的奇偶性的综合应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{2}$ | B. | $\frac{19}{2}$ | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
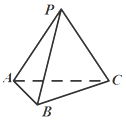 如图,在三棱锥P-ABC中,PA=PC=5,PB=4,AB=BC=2$\sqrt{3}$,∠ACB=30°,PA=PC=5,PB=4,AB=BC=2$\sqrt{3}$,∠ACB=30°.
如图,在三棱锥P-ABC中,PA=PC=5,PB=4,AB=BC=2$\sqrt{3}$,∠ACB=30°,PA=PC=5,PB=4,AB=BC=2$\sqrt{3}$,∠ACB=30°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)在(-∞,-1)上单调递增 | |
| B. | 函数f(x)在(-∞,-1)上单调递减 | |
| C. | 若b=-6,则函数f(x)的图象在点(-2,f(-2))处的切线方程为y=10 | |
| D. | 若b=0,则函数f(x)的图象与直线y=10只有一个公共点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com