本题考查等差数列的通项公式。
思路上,不妨先从小到大,从简到繁进行分析。如果n=2,那么1,2;如果n=3,那么1,2,3;
如果n=4,就应该1,2,3,4;然后将4下一个数,也就是2,去掉。
那么n=69时,本题的解答过程如下:
1,2,3,4,5,……,67,68,69;
第一次去掉所有奇数,余下2,4,6,8,10,12,14,16,……,62,64,66,68;本次,最后一个去掉的是69,那么下一轮的开始,应该跳过2,从4开始。
第二次去掉4,8,12,16,……,64,68(这些是4的倍数),余下2,6,10,14,18,……,58,62,66(被4除余2的数).最后一个去掉数是68,那么下一轮的开始,应该跳过2,从6开始。
第三次,去掉6,14,22,……,62(被8除余6的数),余下2,10,18,26,34,42,50,58,66(被8除余2的数)。最后一个去掉的是62,那么下一轮的开始,应该跳过66,从2开始。
第四次,去掉2,18,34,50,66(被16除余2的数),余下10,26,42,58。最后一个去掉的是66,那么下一轮的开始,跳过10,从26开始。
第五次,去掉26,58;第六次,去掉42,余10.
本题或许还有其他更简洁的解法。如果出题意图本身就是用此种方式考查等差数列的通项公式,那么复杂程度过大,同一知识点反复运用次数过多。



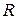 上的偶函数
上的偶函数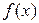 满足:
满足: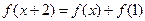 且在区间
且在区间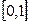 上
上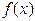 性质的表述:
性质的表述: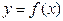 的图象关于直线
的图象关于直线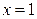 对称; ②函数
对称; ②函数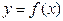 是周期函数;
是周期函数;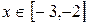 时,
时,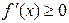 ; ④函数
; ④函数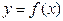 的图象上横坐标为偶数的点都是函数的极小值点。 其中正确表述的番号是 .
的图象上横坐标为偶数的点都是函数的极小值点。 其中正确表述的番号是 .