
分析 (1)由题意,求解y=3-x2(x∈R)的值域,即可得集合A.求解函数 y=$\sqrt{x-2}$+$\frac{2}{{\sqrt{5-x}}}$的定义域即可得B集合.
(2)先(∁UB)的集合,再求A∪(∁UB);
(3集合C={x|5-a<x<a},C⊆(A∩B),求出A∩B,对C进行讨论,求实数a的取值范围.
解答 解:(1)集合A={y|y=3-x2,x∈R},
那么:y=3-x2(x∈R)的值域为(-∞,3];
所以:集合A={y|y≤3}.
函数 y=$\sqrt{x-2}$+$\frac{2}{{\sqrt{5-x}}}$的定义域满足:$\left\{\begin{array}{l}{x-2≥0}\\{5-x>0}\end{array}\right.$,解得:2≤x<5,
所以:集合B={x|2≤x<5}.
(2)∵集合B={x|2≤x<5}.
∴∁UB={x|2>x或x≥5}.
所以:A∪(∁UB)=(-∞,3]∪[5,+∞).
(3)C={x|5-a<x<a},C⊆(A∩B),
∵A∩B={x|2≤x≤3}
当C=∅时,满足题意,则5-a≥a,解得:a$≤\frac{5}{2}$.
当C≠∅时,$\left\{\begin{array}{l}{5-a<a}\\{5-a≥2}\\{a≤3}\end{array}\right.$,解得:$\frac{5}{2}<a≤3$
综合所述:实数a的取值范围是(-∞,3].
点评 本题主要考查集合的确定求法,集合的基本运算,比较基础.属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y平均增加1个单位 | B. | y平均增加2个单位 | ||
| C. | y平均减少1个单位 | D. | y平均减少2个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
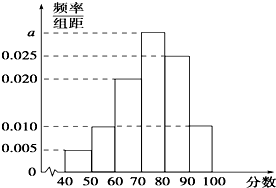 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com