练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设、b为函数

    （I）判断函数上的单调性，并证明你的结论；

    （II）若曲线处的切线斜率为－4，且方程有两个不等的实根，求实数m的取值范围。

    解：（I）依题设方程的两根分别为a、

        （注：写成g(x)在区间（）上单调递增不扣分）                                               

    （II）由，

        的变化情况如下：

    (－∞,－3)

    －3

    －1

    （－1，0）

    0

    ―

    0

    +

    +

    0

    ―

    极小值

    极大值－1

       

           

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设函数f（x）=x2+ax+b（a、b为实常数），已知不等式|f（x）|≤|2x2+4x-6|对任意的实数x均成立．定义数列{an}和{bn}：a1=3，2an=f（an-1）+3（n=2，3，…），bn=
    1
    2+an
    (n=1，2，…)    ，数列{bn}的前n项和Sn．
    （I）求a、b的值；
    （II）求证：Sn＜
    1
    3
    (n∈N*)    ；
    （III ）求证：an＞22n-1-1(n∈N*).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•绵阳三模）已知函数f（x）=2x3-3ax2+a+b（其中a，b为实常数）．
    （I）讨论函数的单调区间；
    （II） 当a＞0时，函数f（x）有三个不同的零点，证明：-a＜b＜a3-a；
    （III） 若f（x）在区间[1，2]上是减函数，设关于X的方程f（x）=2x3-2ax2+3x+a+b的两个非零实数根为x1，x2．试问是否存在实数m，使得m2+tm+1≤|x1-x2|对任意满足条件的a及t∈[-1，1]恒成立？若存在，求m的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•婺城区模拟）已知函数f（x）=ax2-4bx+2alnx（a，b∈R）
    （I）若函数y=f（x）存在极大值和极小值，求
    b
    a
    的取值范围；
    （II）设m，n分别为f（x）的极大值和极小值，若存在实数，b∈（
    e+1
    2
    		e
    a，
    e2+1
    2e
    a），使得m-n=1，求a的取值范围．（e为自然对数的底）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

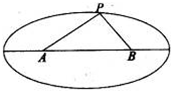    精英家教网如图，两个工厂A，B（视为两个点）相距2km，现要在以A，B为焦点，长轴长为4km的椭圆上某一点P处建一幢办公楼．据测算此办公楼受工厂A的“噪音影响度”与距离AP成反比，比例系数是1；办公楼受工厂B的“噪音影响度”与距离BP也成反比，比例系数是4．办公楼受A，B两厂的“总噪音影响度”y是受A，B两厂“噪音影响度”的和，设AP=xkm．
    （I）求“总噪音影响度”y关于x的函数关系式；
    （II）当AP为多少时，“总噪音影响度”最小？（结果保留一位小数）

    查看答案和解析>>

    同步练习册答案