
设
(1)当 ,求
,求 的取值范围;
的取值范围;
(2)若对任意 ,
, 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
科目:高中数学 来源: 题型:解答题
如图所示,一个半圆和长方形组成的铁皮,长方形的边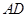 为半圆的直径,
为半圆的直径,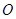 为半圆的圆心,
为半圆的圆心, ,
,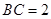 ,现要将此铁皮剪出一个等腰三角形
,现要将此铁皮剪出一个等腰三角形 ,其底边
,其底边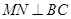 .
.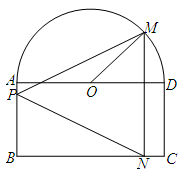
(1)设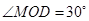 ,求三角形铁皮
,求三角形铁皮 的面积;
的面积;
(2)求剪下的铁皮三角形 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数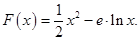
(I)求函数 的最小值;
的最小值;
(II)对于函数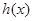 和
和 定义域内的任意实数
定义域内的任意实数 ,若存在常数
,若存在常数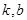 ,使得不等式
,使得不等式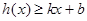 和
和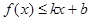 都成立,则称直线
都成立,则称直线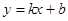 是函数
是函数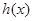 和
和 的“分界线”.
的“分界线”.
设函数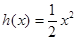 ,
,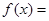
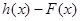 ,试问函数
,试问函数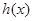 和
和 是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知f(x)= 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)= 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(Ⅰ)已知函数 ,若存在
,若存在 ,使得
,使得 ,则称
,则称 是函数
是函数 的一个不动点,设二次函数
的一个不动点,设二次函数 .
.
(Ⅰ) 当 时,求函数
时,求函数 的不动点;
的不动点;
(Ⅱ) 若对于任意实数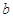 ,函数
,函数 恒有两个不同的不动点,求实数
恒有两个不同的不动点,求实数 的取值范围;
的取值范围;
(Ⅲ) 在(Ⅱ)的条件下,若函数 的图象上
的图象上 两点的横坐标是函数
两点的横坐标是函数 的不动点,且直线
的不动点,且直线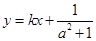 是线段
是线段 的垂直平分线,求实数
的垂直平分线,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某面包厂2011年利润为100万元,因市场竞争,若不开发新项目,预测从2012年起每年利润比上一年减少4万元.2012年初,该面包厂一次性投入90万元开发新项目,预测在未扣除开发所投入资金的情况下,第 年(
年( 为正整数,2012年为第一年)的利润为
为正整数,2012年为第一年)的利润为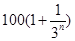 万元.设从2012年起的前
万元.设从2012年起的前 年,该厂不开发新项目的累计利润为
年,该厂不开发新项目的累计利润为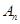 万元,开发新项目的累计利润为
万元,开发新项目的累计利润为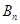 万元(须扣除开发所投入资金).
万元(须扣除开发所投入资金).
(1)求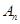 ,
,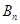 的表达式;
的表达式;
(2)问该新项目的开发是否有效(即开发新项目的累计利润超过不开发新项目的累计利润),如果有效,从第几年开始有效;如果无效,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位设计的两种密封玻璃窗如图所示:图1是单层玻璃,厚度为8 mm;图2是双层中空玻璃,厚度均为4 mm,中间留有厚度为 的空气隔层.根据热传导知识,对于厚度为
的空气隔层.根据热传导知识,对于厚度为 的均匀介质,两侧的温度差为
的均匀介质,两侧的温度差为 ,单位时间内,在单位面积上通过的热量
,单位时间内,在单位面积上通过的热量 ,其中
,其中 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为
为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为 ,空气的热传导系数为
,空气的热传导系数为 .)
.)
(1)设室内,室外温度均分别为 ,
, ,内层玻璃外侧温度为
,内层玻璃外侧温度为 ,外层玻璃内侧温度为
,外层玻璃内侧温度为 ,且
,且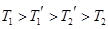 .试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用
.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用 ,
, 及
及 表示);
表示);
(2)为使双层中空玻璃单位时间内,在单位面积上通过的热量只有单层玻璃的4%,应如何设计 的大小?
的大小?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
作为绍兴市2013年5.1劳动节系列活动之一的花卉展在镜湖湿地公园举行.现有一占地1800平方米的矩形地块,中间三个矩形设计为花圃(如图),种植有不同品种的观赏花卉,周围则均是宽为1米的赏花小径,设花圃占地面积为 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)
(1)试将 表示为
表示为 的函数;
的函数;
(2)问应该如何设计矩形地块的边长,使花圃占地面积 取得最大值.
取得最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com