
【题目】下列关于函数![]() 的判断正确的是( )
的判断正确的是( )
①![]() 的解集是
的解集是![]() ;
;
②![]() 极小值,
极小值,![]() 是极大值;
是极大值;
③![]() 没有最小值,也没有最大值.
没有最小值,也没有最大值.
A. ①③ B. ①②③ C. ② D. ①②
【答案】D
【解析】分析:由f(x)>0可解得x的范围,从而确定①正确;
对函数f(x)进行求导,然后令f'(x)=0求出x,在根据f'(x)的正负判断原函数的单调性进而可确定②正确.
根据函数的单调性可判断极大值即是原函数的最大值,无最小值,③不正确.从而得到答案.
详解:由f(x)>0(2x﹣x2)ex>02x﹣x2>00<x<2,故①正确;
f′(x)=ex(2﹣x2),由f′(x)=0得x=±![]() ,
,
由f′(x)<0得x>![]() 或x<﹣
或x<﹣![]() ,
,
由f′(x)>0得﹣![]() <x<
<x<![]() ,
,
∴f(x)的单调减区间为(﹣∞,﹣![]() ),(
),(![]() ,+∞).单调增区间为(﹣,
,+∞).单调增区间为(﹣,![]() ).
).
∴f(x)的极大值为f(![]() ),极小值为f(﹣
),极小值为f(﹣![]() ),故②正确.
),故②正确.
∵x<﹣![]() 时,f(x)<0恒成立.
时,f(x)<0恒成立.
∴f(x)无最小值,但有最大值f(![]() )
)
∴③不正确.
故选:D.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为![]() ,已知摄影爱好者的身高约为
,已知摄影爱好者的身高约为![]() 米(将眼睛S距地面的距离SA按
米(将眼睛S距地面的距离SA按![]() 米处理).
米处理).
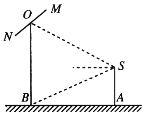
(1)求摄影爱好者到立柱的水平距离AB和立柱的高度OB;
(2)立柱的顶端有一长为2米的彩杆MN,且MN绕其中点O在摄影爱好者与立柱所在的平面内旋转.在彩杆转动的任意时刻,摄影爱好者观察彩杆MN的视角![]() (设为
(设为![]() )是否存在最大值?若存在,请求出
)是否存在最大值?若存在,请求出![]() 取最大值时
取最大值时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(I)求函数在点(1,0)处的切线方程;
(II)设实数k使得f(x)< kx恒成立,求k的范围;
(III)设函数![]() ,求函数h(x)在区间
,求函数h(x)在区间![]() 上的零点个数.
上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域在R上的函数f(x)=|x+1|+|x﹣2|的最小值为a.
(1)求a的值;
(2)若p,q,r为正实数,且p+q+r=a,求证:p2+q2+r2≥3.
查看答案和解析>>
科目:高中数学 来源: 题型:
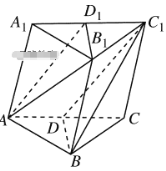
【题目】如图所示,在斜三棱柱ABC—A1B1C1中,点D,D1分别为AC,A1C1上的点.
(1)当![]() 的值等于何值时,BC1∥平面AB1D1;
的值等于何值时,BC1∥平面AB1D1;
(2)若平面BC1D∥平面AB1D1,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产产品![]() 件的总成本
件的总成本![]() (万元).已知产品单价
(万元).已知产品单价![]() (万元)与产品件数
(万元)与产品件数![]() 满足
满足![]() ,生产100件这样的产品单价为50万元.
,生产100件这样的产品单价为50万元.
(1)设产量为![]() 件时,总利润为
件时,总利润为![]() (万元),求
(万元),求![]() 的解析式;
的解析式;
(2)产量![]() 定为多少时总利润
定为多少时总利润![]() (万元)最大?并求最大值.
(万元)最大?并求最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,直线
的长轴长为4,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的右顶点作互相垂直的两条直线
的右顶点作互相垂直的两条直线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 两点(点
两点(点![]() 不同于椭圆
不同于椭圆![]() 的右顶点),证明:直线
的右顶点),证明:直线![]() 过定点
过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差为2,前n项和为Sn , 且S1 , S2 , S4成等比数列.
(1)求数列{an}的通项公式;
(2)令bn=(﹣1)n﹣1 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com