
【题目】如图,在四面体![]() 中,
中,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,二面角
,二面角![]() 为
为![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)证明见解析
(2)![]()
【解析】
(1)取![]() 中点
中点![]() 连接
连接![]() ,得
,得![]()
![]() ,可得
,可得![]() ,
,
可证![]() ,可得
,可得![]() ,进而
,进而![]() 平面
平面![]() ,即可证明结论;
,即可证明结论;
(2)设![]() 分别为边
分别为边![]() 的中点,连
的中点,连![]() ,可得
,可得![]() ,
,![]() ,可得
,可得![]() (或补角)是异面直线
(或补角)是异面直线![]() 与
与![]() 所成的角,
所成的角,![]() ,可得
,可得![]() ,
,![]() 为二面角
为二面角![]() 的平面角,即
的平面角,即![]() ,设
,设![]() ,求解
,求解![]() ,即可得出结论.
,即可得出结论.
(1)证明:取![]() 中点
中点![]() 连接
连接![]() ,
,
由![]() 则
则![]()
![]() ,则
,则![]() ,
,
故![]() ,
,![]() ,
,
![]()
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
故平面![]() 平面
平面![]()
(2)解法一:设![]() 分别为边
分别为边![]() 的中点,
的中点,
则![]() ,
,
![]() (或补角)是异面直线
(或补角)是异面直线![]() 与
与![]() 所成的角.
所成的角.
设![]() 为边
为边![]() 的中点,则
的中点,则![]() ,
,
由![]() 知
知![]() .
.
又由(1)有![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角,
的平面角,![]() ,
,
设![]() 则
则![]()
在![]() 中,
中,![]()
从而![]()
在![]() 中,
中,![]() ,
,
又![]() ,
,
从而在![]() 中,因
中,因![]() ,
,
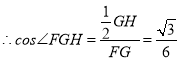 ,
,
因此,异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
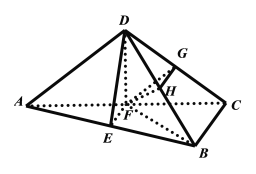
解法二:过点![]() 作
作![]() 交
交![]() 于点
于点![]()
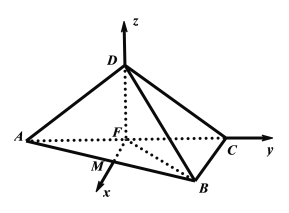
由(1)易知![]() 两两垂直,
两两垂直,
以![]() 为原点,射线
为原点,射线![]() 分别为
分别为![]() 轴,
轴,
![]() 轴,
轴,![]() 轴的正半轴,建立空间直角坐标系
轴的正半轴,建立空间直角坐标系![]() .
.
不妨设![]() ,由
,由![]() ,
,
易知点![]() 的坐标分别为
的坐标分别为![]()
则![]()
显然向量![]() 是平面
是平面![]() 的法向量
的法向量
已知二面角![]() 为
为![]() ,
,
设![]() ,则
,则![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
则
令![]() ,则
,则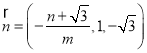
由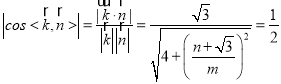
由上式整理得![]() ,
,
解之得![]() (舍)或
(舍)或![]()
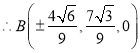
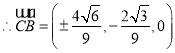 ,
,
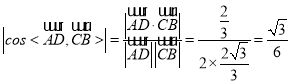
因此,异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】设三棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,
的球面上,![]() 是面积为
是面积为![]() 的等边三角形,
的等边三角形,![]() ,
,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
(1)确定![]() 的位置(需要说明理由),并证明:平面
的位置(需要说明理由),并证明:平面![]() 平面
平面![]() .
.
(2)与侧面![]() 平行的平面
平行的平面![]() 与棱
与棱![]() ,
,![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,
,![]() ,求四面体
,求四面体![]() 的体积的最大值.
的体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
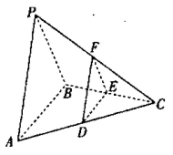
【题目】(2017·江苏高考)如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.

求证:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园划船收费标准如表:

某班16名同学一起去该公园划船,若每人划船的时间均为1小时,每只租船必须坐满,租船最低总费用为______元,租船的总费用共有_____种可能.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某大学学生的某天上网的时间,随机对![]() 名男生和
名男生和![]() 名女生进行了不记名的问卷调查.得到了如下的统计结果:
名女生进行了不记名的问卷调查.得到了如下的统计结果:
表1:男生上网时间与频数分布表
上网时间(分钟) |
|
|
|
|
|
人数 |
|
|
|
|
|
表2:女生上网时间与频数分布表
上网时间(分钟) |
|
|
|
|
|
人数 |
|
|
|
|
|
(1)用分层抽样在![]() 选取
选取![]() 人,再随机抽取
人,再随机抽取![]() 人,求抽取的
人,求抽取的![]() 人都是女生的概率;
人都是女生的概率;
(2)完成下面的![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“大学生上网时间与性别有关”?
的把握认为“大学生上网时间与性别有关”?
上网时间少于 | 上网时间不少于 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: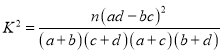
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 表示
表示![]() ,
,![]() 中的最大值,如
中的最大值,如![]()
![]() .已知函数
.已知函数![]() ,
,![]() .
.
(1)设![]() ,求函数
,求函数![]() 在
在![]() 上零点的个数;
上零点的个数;
(2)试探讨是否存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的的参数方程为
的的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() .曲线
.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 作直线
作直线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点(
两点(![]() 在
在![]() 轴上方),求
轴上方),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元五世纪,数学家祖冲之估计圆周率![]() 的值的范围是:3.1415926<
的值的范围是:3.1415926<![]() <3.1415927,为纪念祖冲之在圆周率的成就,把3.1415926称为“祖率”,这是中国数学的伟大成就.某小学教师为帮助同学们了解“祖率”,让同学们把小数点后的7位数字1,4,1,5,9,2,6进行随机排列,整数部分3不变,那么可以得到大于3.14的不同数字有( )
<3.1415927,为纪念祖冲之在圆周率的成就,把3.1415926称为“祖率”,这是中国数学的伟大成就.某小学教师为帮助同学们了解“祖率”,让同学们把小数点后的7位数字1,4,1,5,9,2,6进行随机排列,整数部分3不变,那么可以得到大于3.14的不同数字有( )
A.2280B.2120C.1440D.720
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com