
【题目】设三棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,
的球面上,![]() 是面积为
是面积为![]() 的等边三角形,
的等边三角形,![]() ,
,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
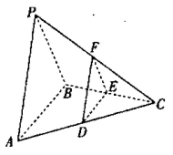
(1)确定![]() 的位置(需要说明理由),并证明:平面
的位置(需要说明理由),并证明:平面![]() 平面
平面![]() .
.
(2)与侧面![]() 平行的平面
平行的平面![]() 与棱
与棱![]() ,
,![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,
,![]() ,求四面体
,求四面体![]() 的体积的最大值.
的体积的最大值.
【答案】(1)![]() 在
在![]() 上,理由见解析,证明见解析,(2)
上,理由见解析,证明见解析,(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,可证
,可证![]() 在线段
在线段![]() 上,
上,![]() 且
且![]() 平面
平面![]() ,从而得到平面
,从而得到平面![]() 平面
平面![]() .
.
(2)设![]() ,可证
,可证![]() ,利用导数可求体积的最大值.
,利用导数可求体积的最大值.
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,取点
,取点![]() 为
为![]() 的三等分点且
的三等分点且![]() ,
,
连接![]() .
.
因为![]() ,所以
,所以![]() .
.
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,故
,故![]() .
.
因为![]() 为等腰直角三角形,
为等腰直角三角形,![]() 为
为![]() 的中点,故
的中点,故![]() ,
,
因为![]() ,
,![]() ,
,
故![]() ,故
,故![]() ,同理
,同理![]() ,
,
因为![]() 是等边三角形,故
是等边三角形,故![]() 为
为![]() 的中心,故
的中心,故![]() ,
,
故![]() 为三棱锥
为三棱锥![]() 的外接球的球心,
的外接球的球心,
故![]() 与
与![]() 重合即
重合即![]() 在线段
在线段![]() 上且
上且![]() .
.

因为![]() 在
在![]() 上,所以
上,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)由题意得![]() ,解得
,解得![]() ,
,
因为![]() 为等腰直角三角形,
为等腰直角三角形,![]() 为
为![]() 的中点,故
的中点,故![]() ,
,
而平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() ,故
,故![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
在等腰直角三角形![]() 中,
中,![]() 即
即![]() 到平面
到平面![]() 的距离
的距离![]() .
.
设![]() ,
,![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
故![]() ,同理
,同理![]() ,因为
,因为![]() 方向相同,故
方向相同,故![]() ,
,
同理![]() ,
,
所以![]() ,则
,则![]() 的面积为
的面积为![]() .
.
又![]() ,所以
,所以![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
所以四面体![]() 的体积
的体积![]() .
.
设![]() ,
,![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 为增函数,在
为增函数,在![]() 为减函数,
为减函数,
所以![]() ,
,
即四面体![]() 的体积的最大值为
的体积的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知动圆![]() 恒过点
恒过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(1)求圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设![]() 是轨迹
是轨迹![]() 上横坐标为2的点,
上横坐标为2的点,![]() 的平行线
的平行线![]() 交轨迹
交轨迹![]() 于
于![]() ,
,![]() 两点,交轨迹
两点,交轨迹![]() 在
在![]() 处的切线于点
处的切线于点![]() ,问:是否存在实常数
,问:是否存在实常数![]() 使
使![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班图书角有文学名著类图书5本,学科辅导书类图书3本,其它类图书2本,共10本不同的图书,该班从图书角的10本不同图书中随机挑选3本不同图书参加学校活动.
(1)求选出的三本图书来自于两个不同类别的概率;
(2)设随机变量X表示选出的3本图书中,文学名著类本数与学科辅导类本数差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月1日我国隆重纪念了建国70周年,期间进行了一系列大型庆祝活动,极大地激发了全国人民的爱国热情.某校高三学生也投入到了这场爱国活动中,他(她)们利用周日休息时间到社区做义务宣讲员,学校为了调查高三男生和女生周日的活动时间情况,随机抽取了高三男生和女生各40人,对他(她)们的周日活动时间进行了统计,分别得到了高三男生的活动时间(单位:小时)的频数分布表和女生的活动时间(单位:小时)的频率分布直方图.(活动时间均在![]() 内)
内)
活动时间 |
|
|
|
|
|
|
频数 | 8 | 10 | 7 | 9 | 4 | 2 |
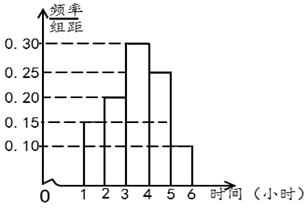
(1)根据调查,试判断该校高三年级学生周日活动时间较长的是男生还是女生?并说明理由;
(2)在被抽取的80名高三学生中,从周日活动时间在![]() 内的学生中抽取2人,求恰巧抽到1男1女的概率.
内的学生中抽取2人,求恰巧抽到1男1女的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为解决城市的拥堵问题,某城市准备对现有的一条穿城公路MON进行分流,已知穿城公路MON自西向东到达城市中心点O后转向东北方向(即![]() ).现准备修建一条城市高架道路L,L在MO上设一出入口A,在ON上设一出入口B.假设高架道路L在AB部分为直线段,且要求市中心O与AB的距离为10km.
).现准备修建一条城市高架道路L,L在MO上设一出入口A,在ON上设一出入口B.假设高架道路L在AB部分为直线段,且要求市中心O与AB的距离为10km.
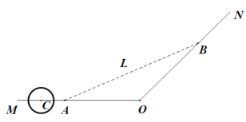
(1)求两站点A,B之间距离的最小值;
(2)公路MO段上距离市中心O30km处有一古建筑群C,为保护古建筑群,设立一个以C为圆心,5km为半径的圆形保护区.则如何在古建筑群C和市中心O之间设计出入口A,才能使高架道路L及其延伸段不经过保护区(不包括临界状态)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①函数![]() 的图象把圆
的图象把圆![]() 的面积两等分
的面积两等分
②![]() 是周期为
是周期为![]() 的函数
的函数
③函数![]() 在区间
在区间![]() 上有3个零点
上有3个零点
④函数![]() 在区间
在区间![]() 上单调递减
上单调递减
其中所有正确结论的编号是( )
A.①③④B.②④C.①④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障某治疗新冠肺炎药品的主要药理成分在国家药品监督管理局规定的值范围内,武汉某制药厂在该药品的生产过程中,检验员在一天中按照规定从该药品生产线上随机抽取20件产品进行检测,测量其主要药理成分含量(单位:mg).根据生产经验,可以认为这条药品生产线正常状态下生产的产品的主要药理成分含量服从正态分布N(μ,σ2).在一天内抽取的20件产品中,如果有一件出现了主要药理成分含量在(μ﹣3σ,μ+3σ)之外的药品,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对本次的生产过程进行检查.
(1)下面是检验员在2月24日抽取的20件药品的主要药理成分含量:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 10.04 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 9.95 | 10.05 | 10.05 | 9.96 | 10.12 |
经计算得![]() xi=9.96,s
xi=9.96,s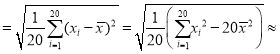 0.19;其中xi为抽取的第i件药品的主要药理成分含量,i=1,2,…,20.用样本平均数
0.19;其中xi为抽取的第i件药品的主要药理成分含量,i=1,2,…,20.用样本平均数![]() 作为μ的估计值
作为μ的估计值![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值![]() ,利用估计值判断是否需对本次的生产过程进行检查?
,利用估计值判断是否需对本次的生产过程进行检查?
(2)假设生产状态正常,记X表示某天抽取的20件产品中其主要药理成分含量在(μ﹣3σ,μ+3σ)之外的药品件数,求/span>P(X=1)及X的数学期望.
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ﹣3σ<Z<μ+3σ)≈0.9974,0.997419≈0.95.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com