
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
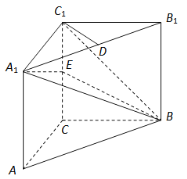
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)![]()
【解析】
(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,证明四边形
,证明四边形![]() 为平行四边形后即可得
为平行四边形后即可得![]() ,再根据线面平行的判定即可得证;
,再根据线面平行的判定即可得证;
(Ⅱ)由等腰三角形的性质和线面垂直的性质可得![]() 、
、![]() ,则可证
,则可证![]() 平面
平面![]() ,再根据面面垂直的判定即可得证;
,再根据面面垂直的判定即可得证;
(Ⅲ)建立空间直角坐标系后,表示出各点坐标,求出平面![]() 的一个法向量为
的一个法向量为![]() ,
,![]() ,利用
,利用![]() 即可得解.
即可得解.
(Ⅰ)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
因为![]() 是
是![]() 的中点,
的中点,
所以![]() ,且
,且![]() ,
,
在三棱柱![]() 中,
中,
因为![]() 是
是![]() 的中点,所以
的中点,所以![]() ,且
,且![]() ,
,
所以![]() 且
且![]() ,
,
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
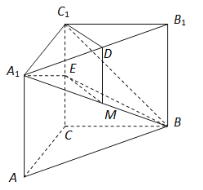
(Ⅱ)证明:因为![]() ,且
,且![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,
,
又 ![]() ,
,![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
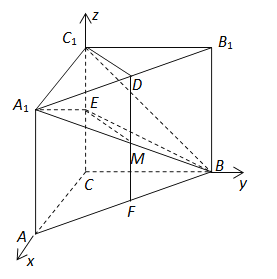
(Ⅲ)如图建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则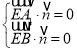 即
即![]() ,
,
令![]() ,则
,则![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则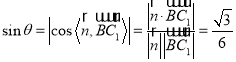 .
.
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x-lnx,g(x)=x2-ax.
(1)求函数f(x)在区间[t,t+1](t>0)上的最小值m(t);
(2)令h(x)=g(x)-f(x),A(x1,h(x1)),B(x2,h(x2))(x1≠x2)是函数h(x)图像上任意两点,且满足![]() >1,求实数a的取值范围;
>1,求实数a的取值范围;
(3)若x∈(0,1],使f(x)≥![]() 成立,求实数a的最大值.
成立,求实数a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网金融的不断发展,很多互联网公司推出余额增值服务产品和活期资金管理服务产品,如蚂蚁金服旗下的“余额宝”,腾讯旗下的“财富通”,京东旗下“京东小金库”.为了调查广大市民理财产品的选择情况,随机抽取1200名使用理财产品的市民,按照使用理财产品的情况统计得到如下频数分布表:
分组 | 频数(单位:名) |
使用“余额宝” |
|
使用“财富通” |
|
使用“京东小金库” | 30 |
使用其他理财产品 | 50 |
合计 | 1200 |
已知这1200名市民中,使用“余额宝”的人比使用“财富通”的人多160名.
(1)求频数分布表中![]() ,
,![]() 的值;
的值;
(2)已知2018年“余额宝”的平均年化收益率为![]() ,“财富通”的平均年化收益率为
,“财富通”的平均年化收益率为![]() .若在1200名使用理财产品的市民中,从使用“余额宝”和使用“财富通”的市民中按分组用分层抽样方法共抽取7人,然后从这7人中随机选取2人,假设这2人中每个人理财的资金有10000元,这2名市民2018年理财的利息总和为
.若在1200名使用理财产品的市民中,从使用“余额宝”和使用“财富通”的市民中按分组用分层抽样方法共抽取7人,然后从这7人中随机选取2人,假设这2人中每个人理财的资金有10000元,这2名市民2018年理财的利息总和为![]() ,求
,求![]() 的分布列及数学期望.注:平均年化收益率,也就是我们所熟知的利息,理财产品“平均年化收益率为
的分布列及数学期望.注:平均年化收益率,也就是我们所熟知的利息,理财产品“平均年化收益率为![]() ”即将100元钱存入某理财产品,一年可以获得3元利息.
”即将100元钱存入某理财产品,一年可以获得3元利息.
查看答案和解析>>
科目:高中数学 来源: 题型:
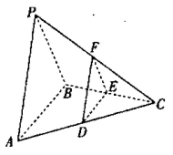
【题目】设三棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,
的球面上,![]() 是面积为
是面积为![]() 的等边三角形,
的等边三角形,![]() ,
,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
(1)确定![]() 的位置(需要说明理由),并证明:平面
的位置(需要说明理由),并证明:平面![]() 平面
平面![]() .
.
(2)与侧面![]() 平行的平面
平行的平面![]() 与棱
与棱![]() ,
,![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,
,![]() ,求四面体
,求四面体![]() 的体积的最大值.
的体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
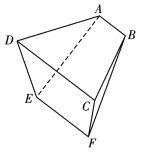
【题目】中国古代数学家刘徽在《九章算术注》中记述:羡除,隧道也,其所穿地,上平下邪.如图所示的五面体![]() 是一个羡除,两个梯形侧面
是一个羡除,两个梯形侧面![]() 与
与![]() 相互垂直,
相互垂直,![]() .若
.若![]() ,
,![]() ,
,![]() ,梯形
,梯形![]() 与
与![]() 的高分别为3和1,则该羡除的体积
的高分别为3和1,则该羡除的体积![]() ( )
( )
A.3B.4C.5D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点为
的焦点为![]() ,
,![]() ,离心率为
,离心率为![]() ,点P为椭圆C上一动点,且
,点P为椭圆C上一动点,且![]() 的面积最大值为
的面积最大值为![]() ,O为坐标原点.
,O为坐标原点.
(1)求椭圆C的方程;
(2)设点![]() ,
,![]() 为椭圆C上的两个动点,当
为椭圆C上的两个动点,当![]() 为多少时,点O到直线MN的距离为定值.
为多少时,点O到直线MN的距离为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·江苏高考)如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.

求证:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的的参数方程为
的的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() .曲线
.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 作直线
作直线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点(
两点(![]() 在
在![]() 轴上方),求
轴上方),求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com