
【题目】随着互联网金融的不断发展,很多互联网公司推出余额增值服务产品和活期资金管理服务产品,如蚂蚁金服旗下的“余额宝”,腾讯旗下的“财富通”,京东旗下“京东小金库”.为了调查广大市民理财产品的选择情况,随机抽取1200名使用理财产品的市民,按照使用理财产品的情况统计得到如下频数分布表:
分组 | 频数(单位:名) |
使用“余额宝” |
|
使用“财富通” |
|
使用“京东小金库” | 30 |
使用其他理财产品 | 50 |
合计 | 1200 |
已知这1200名市民中,使用“余额宝”的人比使用“财富通”的人多160名.
(1)求频数分布表中![]() ,
,![]() 的值;
的值;
(2)已知2018年“余额宝”的平均年化收益率为![]() ,“财富通”的平均年化收益率为
,“财富通”的平均年化收益率为![]() .若在1200名使用理财产品的市民中,从使用“余额宝”和使用“财富通”的市民中按分组用分层抽样方法共抽取7人,然后从这7人中随机选取2人,假设这2人中每个人理财的资金有10000元,这2名市民2018年理财的利息总和为
.若在1200名使用理财产品的市民中,从使用“余额宝”和使用“财富通”的市民中按分组用分层抽样方法共抽取7人,然后从这7人中随机选取2人,假设这2人中每个人理财的资金有10000元,这2名市民2018年理财的利息总和为![]() ,求
,求![]() 的分布列及数学期望.注:平均年化收益率,也就是我们所熟知的利息,理财产品“平均年化收益率为
的分布列及数学期望.注:平均年化收益率,也就是我们所熟知的利息,理财产品“平均年化收益率为![]() ”即将100元钱存入某理财产品,一年可以获得3元利息.
”即将100元钱存入某理财产品,一年可以获得3元利息.
【答案】(1)![]() ;(2)680元.
;(2)680元.
【解析】
(1)根据题意,列方程![]() ,然后求解即可
,然后求解即可
(2)根据题意,计算出10000元使用“余额宝”的利息为![]() (元)和
(元)和
10000元使用“财富通”的利息为![]() (元),
(元),
得到![]() 所有可能的取值为560(元),700(元),840(元),
所有可能的取值为560(元),700(元),840(元),
然后根据![]() 所有可能的取值,计算出相应的概率,并列出
所有可能的取值,计算出相应的概率,并列出![]() 的分布列表,然后求解数学期望即可
的分布列表,然后求解数学期望即可
(1)据题意,得![]() ,
,
所以![]() .
.
(2)据![]() ,得这被抽取的7人中使用“余额宝”的有4人,使用“财富通”的有3人.
,得这被抽取的7人中使用“余额宝”的有4人,使用“财富通”的有3人.
10000元使用“余额宝”的利息为![]() (元).
(元).
10000元使用“财富通”的利息为![]() (元).
(元).
![]() 所有可能的取值为560(元),700(元),840(元).
所有可能的取值为560(元),700(元),840(元).
![]() ,
,![]() ,
,![]() .
.
![]() 的分布列为
的分布列为
| 560 | 700 | 840 |
|
|
|
|
所以![]() (元).
(元).


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】图一是美丽的“勾股树”,它是一个直角三角形分别以它的每一边向外作正方形而得到.图二是第1代“勾股树”,重复图二的作法,得到图三为第2代“勾股树”,以此类推,已知最大的正方形面积为1,则第![]() 代“勾股树”所有正方形的个数与面积的和分别为( )
代“勾股树”所有正方形的个数与面积的和分别为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若满足
,若满足![]() ,则称函数
,则称函数![]() 为“
为“![]() 型函数”.
型函数”.
(1)判断函数![]() 和
和![]() 是否为“
是否为“![]() 型函数”,并说明理由;
型函数”,并说明理由;
(2)设函数![]() ,记
,记![]() 为函数
为函数![]() 的导函数.
的导函数.
①若函数![]() 的最小值为1,求
的最小值为1,求![]() 的值;
的值;
②若函数![]() 为“
为“![]() 型函数”,求
型函数”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月,甲乙两校的学生参加了某考试机构举行的大联考,现对这两校参加考试的学生的数学成绩进行统计分析,数据统计显示,考生的数学成绩![]() 服从正态分布
服从正态分布![]() ,从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷,并将这40份试卷的得分制作成如图所示的茎叶图:
,从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷,并将这40份试卷的得分制作成如图所示的茎叶图:
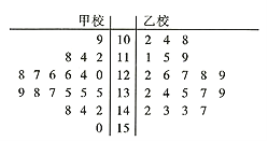
(1)试通过茎叶图比较这40份试卷的两校学生数学成绩的中位数;
(2)若把数学成绩不低于135分的记作数学成绩优秀,根据茎叶图中的数据,判断是否有![]() 的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关?
的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关?
(3)从所有参加此次联考的学生中(人数很多)任意抽取3人,记数学成绩在134分以上的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() .
.
参考公式与临界值表:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】意大利人斐波那契在1202年写的《计算之书》中提出一个兔子繁殖问题:假设一对刚出生的小兔一个月后能长成大兔,再过一个月便能生下一对小兔,此后每个月生一对小兔,如此,设第n个月的兔子对数为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,….考查数列
,….考查数列![]() 的规律,不难发现,
的规律,不难发现,![]() (
(![]() ),我们称该数列为斐波那契数列.
),我们称该数列为斐波那契数列.
(1)若数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() ,
,![]() (
(![]() ,
,![]() ),试判断数列
),试判断数列![]() 是否构成斐波那契数列,说明理由;
是否构成斐波那契数列,说明理由;
(2)若数列![]() 是斐波那契数列,且
是斐波那契数列,且![]() ,求证:数列
,求证:数列![]() 是等比数列;
是等比数列;
(3)若数列![]() 是斐波那契数列,求数列
是斐波那契数列,求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场有一块农田,如图所示,它的边界由圆O的一段圆弧![]() (P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为
(P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为![]() ,要求
,要求![]() 均在线段
均在线段![]() 上,
上,![]() 均在圆弧上.设OC与MN所成的角为
均在圆弧上.设OC与MN所成的角为![]() .
.
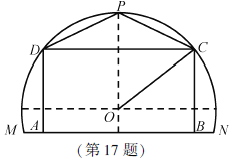
(1)用![]() 分别表示矩形
分别表示矩形![]() 和
和![]() 的面积,并确定
的面积,并确定![]() 的取值范围;
的取值范围;
(2)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为![]() .求当
.求当![]() 为何值时,能使甲、乙两种蔬菜的年总产值最大.
为何值时,能使甲、乙两种蔬菜的年总产值最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学组织高二年级开展对某品牌西瓜市场调研活动.两名同学经过了解得知此品牌西瓜,不仅便宜而且口味还不错,并且每日的销售量y(单位:千克)与销售价格x(元/千克)满足关系式:![]() ,其中
,其中![]() ,a为常数.已知销售价格为5元/千克时,每日可售出此品牌西瓜11千克.若此品牌西瓜的成本为3元/千克,试确定销售价格x的值,使该商场日销售此品牌西瓜所获得的利润最大.
,a为常数.已知销售价格为5元/千克时,每日可售出此品牌西瓜11千克.若此品牌西瓜的成本为3元/千克,试确定销售价格x的值,使该商场日销售此品牌西瓜所获得的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四面体![]() 的棱长满足
的棱长满足![]() ,
,![]() ,现将四面体
,现将四面体![]() 放入一个主视图为等边三角形的圆锥中,使得四面体
放入一个主视图为等边三角形的圆锥中,使得四面体![]() 可以在圆锥中任意转动,则圆锥侧面积的最小值为___________.
可以在圆锥中任意转动,则圆锥侧面积的最小值为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】气象意义上,从春季进入夏季的标志为:“连续5天的日平均温度不低于22℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据的中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com