
分析 (1)利用函数的单调性的定义证明即可.
(2)通过函数的单调性,然后求解闭区间的函数的最值即可.
解答 解:(1)f(x)在[1,+∞)上是增函数. ….(1分)
证明如下:在[1,+∞)上任取x1,x2且x1<x2,那么$f({x_1})-f({x_2})=\frac{{2{x_1}+1}}{{{x_1}+1}}-\frac{{2{x_2}+1}}{{{x_2}+1}}$=$\frac{{2{x_1}{x_2}+{x_2}+2{x_1}+1-2{x_1}{x_2}-2{x_2}-{x_1}-1}}{{({x_1}+1)({x_2}+1)}}$=$\frac{{{x_1}-{x_2}}}{{({x_1}+1)({x_2}+1)}}$…..(5分)
因为x1<x2,所以x1-x2<0
又x1≥1,x2≥1所以x1+1>0,x2+1>0
所以$\frac{{{x_1}-{x_2}}}{{({x_1}+1)({x_2}+1)}}<0$…..(7分)
即f(x1)-f(x2)<0,所以f(x1)<f(x2),
所以f(x)在[1,+∞)上是增函数. …..(8分)
(2)因为[1,3]⊆[1,+∞)且f(x)在[1,+∞)上是增函数,
所以f(x)在[1,3]上是增函数,
则$f{(x)_{max}}=f(3)=\frac{7}{4},f{(x)_{min}}=f(1)=\frac{3}{2}$.
点评 本题考查函数的单调性的判断与证明,单调性的应用,函数的最值的求法,考查计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {-2} | C. | {-2,2} | D. | {-2,0,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 5$\sqrt{2}$ | C. | 2$\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
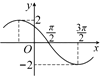 已知f(x)=Asin(ωx+φ),(A>0,ω>0,φ∈(0,π)),其导函数f'(x)的部分图象如图所示,则下列对f(x)的说法正确的是( )
已知f(x)=Asin(ωx+φ),(A>0,ω>0,φ∈(0,π)),其导函数f'(x)的部分图象如图所示,则下列对f(x)的说法正确的是( )| A. | 最大值为4且关于直线$x=-\frac{π}{2}$对称 | |
| B. | 最大值为4且在$[{-\frac{π}{2}\;\;,\;\;\frac{π}{2}}]$上单调递增 | |
| C. | 最大值为2且关于点$({-\frac{π}{2}\;\;,\;\;0})$中心对称 | |
| D. | 最大值为2且在$[{-\frac{π}{2}\;\;,\;\;\frac{3π}{2}}]$上单调递减 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com