
分析 根据斜截式的适用范围,可判断①;根据过原点的直线两截距也相等,可判断②;求出函数的最小值,可判断③;求出直线m的倾斜角,可判断④;求出轨迹方程,可判断⑤.
解答 解:①方程y=kx+2可表示经过点(0,2)且斜率存在的直线,不包括y轴,故错误;
②过点P(3,-4),且截距相等的直线方程为x+y-1=0,或4x+3y=0,故错误;
③函数y=$\sqrt{{x^2}+1}$+$\sqrt{{x^2}-4x+13}$表示动点P(x,0)到两定点A(0,1)和B(2,-3)的距离和,
当P落在AB与x轴的交点($\frac{1}{2}$,0)处时,取最小值2$\sqrt{5}$,故正确;
④平行线l1:x-y+1=0与l2:x-y+3=0的倾斜角为45°,且距离为$\sqrt{2}$
若直线m被两平行线l1:x-y+1=0与l2:x-y+3=0所截得的线段长为2$\sqrt{2}$,
则m与l1的夹角为30°,则m的倾斜角可以是15°或75°,故正确;
⑤点P(4,-2)与圆x2+y2=4上任一点连线段的中点M的坐标设为(x,y),
圆x2+y2=4上对应点设为(a,b),
则a=2x-4,b=2y+2,则(2x-4)2+(2y+2)2=4,
故M点的轨迹方程为(x-2)2+(y+1)2=1.故错误;
故答案为:③④.
点评 本题以命题的真假判断与应用为载体,考查了直线方程,直接的倾斜角,轨迹方程等知识点,难度中档.


科目:高中数学 来源: 题型:选择题
 用5种不同颜色给图中的4个区域涂色,每个区域涂1种颜色,相邻区域不能同色,求不同的涂色方法共有多少种( )
用5种不同颜色给图中的4个区域涂色,每个区域涂1种颜色,相邻区域不能同色,求不同的涂色方法共有多少种( )| A. | 120 | B. | 150 | C. | 180 | D. | 240 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 8 | C. | 4 | D. | -8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
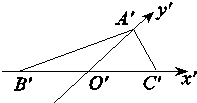 已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=$\frac{\sqrt{3}}{2}$,那么原△ABC中∠ABC的大小是( )
已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=$\frac{\sqrt{3}}{2}$,那么原△ABC中∠ABC的大小是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{17}$ | B. | $\sqrt{41}$ | C. | $\sqrt{17}$或$\sqrt{41}$ | D. | $\sqrt{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2014}$-1 | B. | $\sqrt{2015}$-1 | C. | $\sqrt{2016}$-1 | D. | $\sqrt{2017}$-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com