解:(Ⅰ)当点M第一次由点A按逆时针方向运动到定点C时,所形成的角为α=

,
第二次由点A按逆时针方向运动到定点D时,所形成的角为β=

,
则cos(α-β)=cos

=cos(

-

)=cos

cos

+sin

sin

=
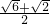
;
(Ⅱ)存在,当点M第一次由点A按逆时针方向运动到定点B,
第二次由点A按逆时针方向运动到定点F时,角α=

,β=

,满足题意,
理由如下:
由
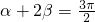
,得到

+β=

,
∵
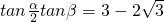
,
∴tan(

+β)=
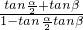
=
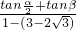
=-1,
∴tan

+tanβ=2-2

,
∴tan

=-

,tanβ=2-

或tan

=2-

,tanβ=-

,
当

=

,β=

,不满足题意;
当

=

,即α=

,β=

时,满足题意,
则M第一次由点A按逆时针方向运动到某定点B,
第二次由点A按逆时针方向运动到定点F时满足题意.
分析:(Ⅰ)根据C的坐标及C在第一象限,得到tanα的值,利用特殊角的三角函数值求出C的度数,即为α的度数;同理根据D的坐标,及第二次由点A按逆时针方向运动到某定点D,得到β的度数,代入cos(α-β),把角

变形为

-

,利用两角和与差的余弦函数公式及特殊角的三角函数值即可求出值;
(Ⅱ)存在两点B和F,满足题意,理由为:由已知的α+2β的度数求出
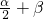
的度数,然后利用两角和与差的正切函数公式及特殊角的三角函数值化简tan(
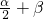
),把
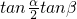
的值及
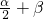
的度数代入,求出

的值,两者联立分别求出

的值,根据特殊角的三角函数值即可得到α,β的度数,进而找出对应的点.
点评:此题考查了三角函数恒等式的证明,涉及的知识有两角和与差的正切、余弦函数公式,点与坐标系,锐角三角函数定义,以及特殊角的三角函数值,熟练掌握公式是解本题的关键.

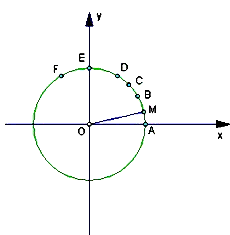 如图,圆O为单位圆,A(1,0),
如图,圆O为单位圆,A(1,0),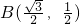 ,
,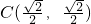 ,
,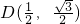 ,E(0,1),
,E(0,1),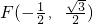 为圆O上的定点,点M为圆O上的动点.M第一次由点A按逆时针方向运动到某定点,所形成的角为α;M第二次由点A按逆时针方向运动到某定点,所形成的角为β.
为圆O上的定点,点M为圆O上的动点.M第一次由点A按逆时针方向运动到某定点,所形成的角为α;M第二次由点A按逆时针方向运动到某定点,所形成的角为β.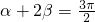 ,且
,且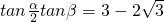 .若不存在,说明理由; 若存在,找出定点并证明.
.若不存在,说明理由; 若存在,找出定点并证明. ,
, ,
,
 -
- )=cos
)=cos cos
cos +sin
+sin sin
sin =
=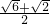 ;
; ,β=
,β= ,满足题意,
,满足题意,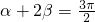 ,得到
,得到 +β=
+β= ,
,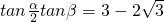 ,
, +β)=
+β)=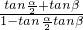 =
=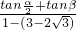 =-1,
=-1, +tanβ=2-2
+tanβ=2-2 ,
, =-
=- ,tanβ=2-
,tanβ=2- 或tan
或tan =2-
=2- ,tanβ=-
,tanβ=- ,
, =
= ,β=
,β= ,不满足题意;
,不满足题意; =
= ,即α=
,即α= ,β=
,β= 时,满足题意,
时,满足题意, 变形为
变形为 -
- ,利用两角和与差的余弦函数公式及特殊角的三角函数值即可求出值;
,利用两角和与差的余弦函数公式及特殊角的三角函数值即可求出值;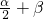 的度数,然后利用两角和与差的正切函数公式及特殊角的三角函数值化简tan(
的度数,然后利用两角和与差的正切函数公式及特殊角的三角函数值化简tan(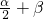 ),把
),把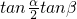 的值及
的值及 的度数代入,求出
的度数代入,求出 的值,两者联立分别求出
的值,两者联立分别求出 的值,根据特殊角的三角函数值即可得到α,β的度数,进而找出对应的点.
的值,根据特殊角的三角函数值即可得到α,β的度数,进而找出对应的点.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案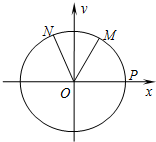 如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,∠POM=
如图,设P是单位圆和x轴正半轴的交点,M、N是单位圆上的两点,O是坐标原点,∠POM= 如图A,B是单位圆O上的点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形.若A点的坐标为(
如图A,B是单位圆O上的点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形.若A点的坐标为( [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内. 如图,圆O为单位圆,A(1,0),B(
如图,圆O为单位圆,A(1,0),B(