(1)对于集合P
7 ,有n=7.当k=4时,P
n={
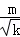
|m∈I
n,k∈I
n}中有3个数(1,2,3)与
I
n={1,2,3…,n}中的数重复,由此求得
集合P
7中元素的个数为 7×7﹣3=46.
(2)先证当n≥15时,P
n不能分成两个不相交的稀疏集的并集.否则,设A和B为两个不相交的稀疏集,使A∪B=P
n?I
n .
不妨设1∈A,则由于1+3=2
2,∴3∉A,即3∈B.同理可得,6∈A,10∈B.又推出15∈A,但1+15=4
2,
这与A为稀疏集相矛盾.
再证P
14满足要求.当k=1时,P
14={
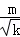
|m∈I
14,k∈I
14}=I
14,可以分成2个稀疏集的并集.
事实上,只要取A
1={1,2,4,6,9,11,13},B
1={3,5,7,8,10,12,14},则A
1和B
1都是稀疏集,且A
1∪B
1=I
14.
当k=4时,集合{
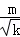
|m∈I
14}中,除整数外,剩下的数组成集合{

,
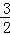
,
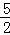
,…,
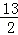
},可以分为下列3个稀疏集的并:
A
2={
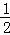
,

,
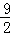
,
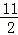
},B
2={
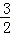
,
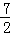
,
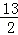
}.
当k=9时,集合{
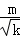
|m∈I
14}中,除整数外,剩下的数组成集合{
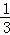
,
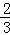
,
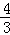
,
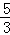
,…,
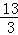
,
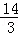
},
可以分为下列3个稀疏集的并:
A
3={

,
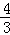
,
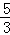
,
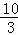
,
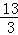
},B
3={
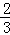
,
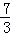
,
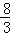
,
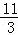
,
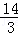
}.
最后,集合C═{
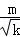
|m∈I
14,k∈I
14,且k≠1,4,9 }中的数的分母都是无理数,
它与P
n中的任何其他数之和都不是整数,
因此,令A=A
1∪A
2∪A
3∪C,B=B
1∪B
2∪B
3,则A和B是不相交的稀疏集,且A∪B=P
14.
综上可得,n的最大值为14.

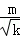 |m∈In,k∈In}.
|m∈In,k∈In}.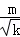 |m∈In,k∈In}中有3个数(1,2,3)与
|m∈In,k∈In}中有3个数(1,2,3)与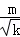 |m∈I14,k∈I14}=I14,可以分成2个稀疏集的并集.
|m∈I14,k∈I14}=I14,可以分成2个稀疏集的并集.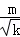 |m∈I14}中,除整数外,剩下的数组成集合{
|m∈I14}中,除整数外,剩下的数组成集合{ ,
,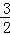 ,
,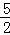 ,…,
,…,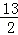 },可以分为下列3个稀疏集的并:
},可以分为下列3个稀疏集的并: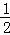 ,
, ,
,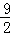 ,
,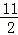 },B2={
},B2={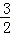 ,
,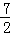 ,
,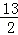 }.
}.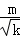 |m∈I14}中,除整数外,剩下的数组成集合{
|m∈I14}中,除整数外,剩下的数组成集合{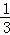 ,
,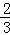 ,
,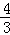 ,
,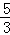 ,…,
,…,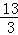 ,
,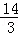 },
}, ,
,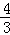 ,
,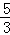 ,
,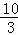 ,
,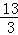 },B3={
},B3={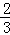 ,
,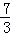 ,
,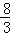 ,
,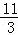 ,
,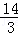 }.
}.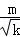 |m∈I14,k∈I14,且k≠1,4,9 }中的数的分母都是无理数,
|m∈I14,k∈I14,且k≠1,4,9 }中的数的分母都是无理数,

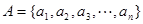
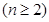 .如果
.如果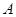 中元素
中元素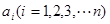 满足
满足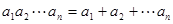 ,就称
,就称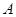 为“复活集”,给出下列结论:
为“复活集”,给出下列结论: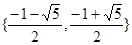 是“复活集”;
是“复活集”;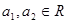 ,且
,且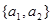 是“复活集”,则
是“复活集”,则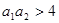 ;
;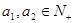 ,则
,则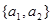 不可能是“复活集”;
不可能是“复活集”;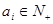 ,则“复合集”
,则“复合集”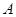 有且只有一个,且
有且只有一个,且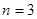 .
.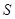 是整数集
是整数集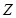 的非空子集,如果
的非空子集,如果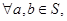 有
有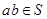 ,则称
,则称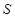 关于数的乘法是封闭的. 若
关于数的乘法是封闭的. 若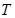 ,
,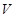 是
是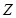 的两个不相交的非空子集,
的两个不相交的非空子集,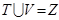 且
且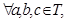 有
有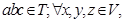 有
有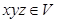 ,有四个命题:①
,有四个命题:①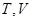 中至少有一个关于乘法是封闭的;②
中至少有一个关于乘法是封闭的;②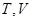 中至多有一个关于乘法是封闭的;③
中至多有一个关于乘法是封闭的;③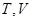 中有且只有一个关于乘法是封闭的;④
中有且只有一个关于乘法是封闭的;④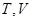 中每一个关于乘法都是封闭的.其中所有正确命题的序号是 .
中每一个关于乘法都是封闭的.其中所有正确命题的序号是 .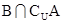 =( )
=( )