练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】函数f（x）= 的定义域是（ ）
    A.[4，+∞）
    B.（﹣∞，4]
    C.（3，+∞）
    D.（3，4]

    【答案】D
    【解析】解：要使函数的解析式有意义 自变量x须满足：log0.5（x﹣3）≥0且x﹣3＞0，
    ∴0＜x﹣3≤1
    解得3＜x≤4
    故函数f（x）的定义域为（3，4]
    故选：D
    【考点精析】本题主要考查了函数的定义域及其求法的相关知识点，需要掌握求函数的定义域时，一般遵循以下原则：①是整式时，定义域是全体实数;②是分式函数时，定义域是使分母不为零的一切实数;③是偶次根式时，定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1,零（负）指数幂的底数不能为零才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，设动点P到定点F（1，0）的距离与到定直线l：x=﹣1的距离相等，记P的轨迹为Γ．又直线AB的一个方向向量 且过点（1，0），AB与Γ交于A、B两点，求|AB|的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于x的二次方程x2+2mx+2m+1=0．
    （Ⅰ）若方程有两根，其中一根在区间（﹣1，0）内，另一根在区间（1，2）内，求m 的取值范围．
    （Ⅱ）若方程两根均在区间（0，1）内，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（x2﹣3x+3）ex的定义域为[﹣2，t]，设f（﹣2）=m，f（t）=n．
    （1）试确定t的取值范围，使得函数f（x）在[﹣2，t]上为单调函数；
    （2）求证：m＜n；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部ABCD是矩形，其中AB=2米，BC=1米；上部CDG是等边三角形，固定点E为AB的中点．△EMN是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆．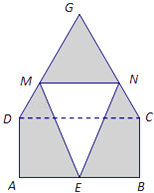

    （1）设MN与AB之间的距离为x米，试将△EMN的面积S（平方米）表示成关于x的函数；
    （2）求△EMN的面积S（平方米）的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2x﹣1+a，g（x）=bf（1﹣x），其中a，b∈R，若关于x的不等式f（x）≥g（x）的解的最小值为2，则实数a的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知△ABC的周长为 +1，且sinA+sinB= sinC （I）求边AB的长；
    （Ⅱ）若△ABC的面积为 sinC，求角C的度数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={x|1＜2x﹣1＜7}，集合B={x|x2﹣2x﹣3＜0}．
    （1）求A∩B；
    （2）求R（A∪B）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱ABC﹣A1B1C1中，侧面ABB1A1 ， ACC1A1均为正方形，∠BAC=90°，点D是棱B1C1的中点．请建立适当的坐标系，求解下列问题： （Ⅰ）求证：异面直线A1D与BC互相垂直；
    （Ⅱ）求二面角（钝角）D﹣A1C﹣A的余弦值．

    查看答案和解析>>

    同步练习册答案