
【题目】已知关于x的二次方程x2+2mx+2m+1=0.
(Ⅰ)若方程有两根,其中一根在区间(﹣1,0)内,另一根在区间(1,2)内,求m 的取值范围.
(Ⅱ)若方程两根均在区间(0,1)内,求m的取值范围.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:
【题目】某地区的农产品A第x天(1≤x≤20,x∈N*)的销售价格p=50﹣|x﹣6|(元∕百斤),一农户在第x天(1≤x≤20,x∈N*)农产品A的销售量q=a+|x﹣8|(百斤)(a为常数),且该农户在第7天销售农产品A的销售收入为2009元.
(1)求该农户在第10天销售农产品A的销售收入是多少?
(2)这20天中该农户在哪一天的销售收入最大?为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在(﹣∞,+∞)上的偶函数,且在 (﹣∞,0]上是增函数,设a=f(log47),b=f( ![]() ),c=f(0.20.6),则a,b,c大小关系是 .
),c=f(0.20.6),则a,b,c大小关系是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=kax﹣a﹣x(a>0且a≠1)是奇函数.
(1)求常数k的值;
(2)若a>1,试判断函数f(x)的单调性,并加以证明;
(3)若已知f(1)= ![]() ,且函数g(x)=a2x+a﹣2x﹣2mf(x)在区间[1,+∞)上的最小值为﹣2,求实数m的值.
,且函数g(x)=a2x+a﹣2x﹣2mf(x)在区间[1,+∞)上的最小值为﹣2,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.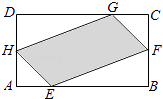
(1)写出y关于x的函数关系式,并指出这个函数的定义域;
(2)当AE为何值时,绿地面积y最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,x,y∈R,证明:(a2+b2)(x2+y2)≥(ax+by)2 , 并利用上述结论求(m2+4n2)( ![]() +
+ ![]() )的最小值(其中m,n∈R且m≠0,n≠0).
)的最小值(其中m,n∈R且m≠0,n≠0).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A城市的出租车计价方式为:若行程不超过3千米,则按“起步价”10元计价;若行程超过3千米,则之后2千米以内的行程按“里程价”计价,单价为1.5元/千米;若行程超过5千米,则之后的行程按“返程价”计价,单价为2.5元/千米.设某人的出行行程为x千米,现有两种乘车方案:①乘坐一辆出租车;②每5千米换乘一辆出租车.
(Ⅰ)分别写出两种乘车方案计价的函数关系式;
(Ⅱ)对不同的出行行程,①②两种方案中哪种方案的价格较低?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com