Question

【题目】如图，有一块矩形空地，要在这块空地上开辟一个内接四边形为绿地，使其四个顶点分别落在矩形的四条边上，已知AB=a（a＞2），BC=2，且AE=AH=CF=CG，设AE=x，绿地面积为y．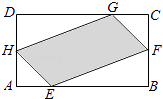

（1）写出y关于x的函数关系式，并指出这个函数的定义域；
（2）当AE为何值时，绿地面积y最大？

Answer 1

【答案】
（1）解：依题意， ，

，

∴ ，

由题意 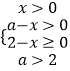，解得：0＜x≤2，

∴y=﹣2x2+（a+2）x，其中0＜x≤2

（2）解：∵y=﹣2x2+（a+2）x的图象为抛物线，其开口向下、对称轴是 ，

∴y=﹣2x2+（a+2）x在上 递增，在 上递减，

若 ，即a＜6，则 时，y取最大值 ；

若 ，即a≥6，则y=﹣2x2+（a+2）x，0＜x≤2是增函数，

故当x=2时，y取最大值2a﹣4；

综上所述：若a＜6，则 时绿地面积取最大值 ；

若a≥6，则AE=2时绿地面积取最大值2a﹣4．

【解析】（1）根据题意不难得出,,不难得出y关于x的解析式，再根据各边长大于0，得出x的定义域，（2）根据（1）中的解析式，由二次函数求最值的方法可得到AE=2时，绿地面积y最大.