
【题目】在直角坐标系xOy中,设动点P到定点F(1,0)的距离与到定直线l:x=﹣1的距离相等,记P的轨迹为Γ.又直线AB的一个方向向量 ![]() 且过点(1,0),AB与Γ交于A、B两点,求|AB|的长.
且过点(1,0),AB与Γ交于A、B两点,求|AB|的长.
【答案】解:∵动点P到定点F(1,0)的距离与到定直线l:x=﹣1的距离相等,
∴由抛物线的定义,可得动点P的轨迹Γ是抛物线,
设其方程为y2=2px,由 ![]() =1得2p=4,
=1得2p=4,
∴抛物线的方程为y2=4x,即为曲线Γ的方程.
∵直线AB的一个方向向量 ![]() ,过点(1,0),
,过点(1,0),
∴直线AB的斜率k=2,方程为y=2(x﹣1),即y=2x﹣2.
设直线l与曲线Γ的交点坐标为A(x1 , y1)、B(x2 , y2),
由 ![]() ,整理得x2﹣3x+1=0,可得x1+x2=3.
,整理得x2﹣3x+1=0,可得x1+x2=3.
∴根据抛物线的定义,可得|AB|=x1+x2+p=2+x1+x2=5.
【解析】根据抛物线的定义得动点P的轨迹Γ是抛物线,求出其方程为y2=4x.由直线方程的点斜式,算出直线AB的方程为y=2x﹣2,再将直线方程与抛物线方程联解,并结合抛物线的定义加以计算,可得线段AB的长.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】(用空间向量坐标表示解答)如图,在直三棱柱ABC﹣A1B1C1中,AC=BC=CC1=2,AC⊥BC,D为AB的中点. 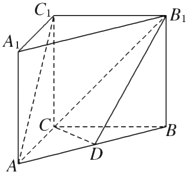
(1)求证:AC1∥面B1CD
(2)求直线AA1与面B1CD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区的农产品A第x天(1≤x≤20,x∈N*)的销售价格p=50﹣|x﹣6|(元∕百斤),一农户在第x天(1≤x≤20,x∈N*)农产品A的销售量q=a+|x﹣8|(百斤)(a为常数),且该农户在第7天销售农产品A的销售收入为2009元.
(1)求该农户在第10天销售农产品A的销售收入是多少?
(2)这20天中该农户在哪一天的销售收入最大?为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式(4kx﹣k2﹣12k﹣9)(2x﹣11)>0,其中k∈R;
(1)试求不等式的解集A;
(2)对于不等式的解集A,记B=A∩Z(其中Z为整数集),若集合B为有限集,求实数k的取值范围,使得集合B中元素个数最少,并用列举法表示集合B.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知ABCD﹣A1B1C1D1为正方体,① ![]() ;②
;② ![]() ;③向量
;③向量 ![]() 与向量
与向量 ![]() 的夹角是60°;④正方体ABCD﹣A1B1C1D1的体积为
的夹角是60°;④正方体ABCD﹣A1B1C1D1的体积为 ![]() .其中正确的命题是(写出所有正确命题编号)
.其中正确的命题是(写出所有正确命题编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在(﹣∞,+∞)上的偶函数,且在 (﹣∞,0]上是增函数,设a=f(log47),b=f( ![]() ),c=f(0.20.6),则a,b,c大小关系是 .
),c=f(0.20.6),则a,b,c大小关系是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=kax﹣a﹣x(a>0且a≠1)是奇函数.
(1)求常数k的值;
(2)若a>1,试判断函数f(x)的单调性,并加以证明;
(3)若已知f(1)= ![]() ,且函数g(x)=a2x+a﹣2x﹣2mf(x)在区间[1,+∞)上的最小值为﹣2,求实数m的值.
,且函数g(x)=a2x+a﹣2x﹣2mf(x)在区间[1,+∞)上的最小值为﹣2,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com