
【题目】(用空间向量坐标表示解答)如图,在直三棱柱ABC﹣A1B1C1中,AC=BC=CC1=2,AC⊥BC,D为AB的中点. 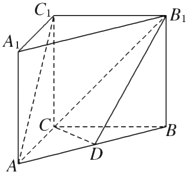
(1)求证:AC1∥面B1CD
(2)求直线AA1与面B1CD所成角的正弦值.
【答案】
(1)证明:以C为坐标原点,以CA,CB,CC1为坐标轴建立空间直角坐标系,如图所示:
则A(2,0,0),C1(0,0,2),C(0,0,0),D(1,1,0),B1(0,2,2),
∴ ![]() =(﹣2,0,2),
=(﹣2,0,2), ![]() =(1,1,0),
=(1,1,0), ![]() =(0,2,2).
=(0,2,2).
设平面B1CD的法向量为 ![]() =(x,y,z).则
=(x,y,z).则 ![]() ,
, ![]() =0,
=0,
∴ ![]() ,令z=1,得
,令z=1,得 ![]() =(1,﹣1,1).
=(1,﹣1,1).
∴ ![]() =﹣2+0+2=0,
=﹣2+0+2=0,
∵AC1平面B1CD,
∴AC1∥面B1CD.

(2)解: ![]() =
= ![]() =(0,0,2),
=(0,0,2),
∴ ![]() =2,|
=2,| ![]() |=2,
|=2, ![]() =
= ![]() ,
,
∴cos< ![]() ,
, ![]() >=
>=  =
= ![]() .
.
∴直线AA1与面B1CD所成角的正弦值为 ![]() .
.
【解析】(1)以C为坐标原点建立空间直角坐标系,求出平面B1CD的法向量 ![]() ,只需证明
,只需证明 ![]() ⊥
⊥ ![]() 即可;(2)直线AA1与面B1CD所成角的正弦值为|cos<
即可;(2)直线AA1与面B1CD所成角的正弦值为|cos< ![]() ,
, ![]() >|.
>|.
【考点精析】本题主要考查了直线与平面平行的判定和空间角的异面直线所成的角的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】设全集为R,A={x|2x2﹣9x+4≤0},B={x|x2+a<0}.
(1)当a=﹣9时,求A∩B,(RA)∪B;
(2)当a<0时,若(RA)∩B=B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数Z=(m2+5m+6)+(m2﹣2m﹣15)i,当实数m为何值时:
(1)Z为实数;
(2)Z为纯虚数;
(3)复数Z对应的点Z在第四象限.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)= ![]() (a>0且a≠1)
(a>0且a≠1)
(1)若a=2,解不等式f(x)≤5;
(2)若函数f(x)的值域是[4,+∞),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1 , ∠BAA1=60° 
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C= ![]() ,求三棱柱ABC﹣A1B1C1的体积.
,求三棱柱ABC﹣A1B1C1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间直角坐标系中有直三棱柱ABC﹣A1B1C1 , CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( )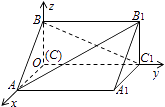
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市上年度电价为0.80元/千瓦时,年用电量为a千瓦时.本年度计划将电价降到0.55元/千瓦时~0.75元/千瓦时之间,而居民用户期望电价为0.40元/千瓦时(该市电力成本价为0.30元/千瓦时)经测算,下调电价后,该城市新增用电量与实际电价和用户期望电价之差成反比,比例系数为0.2a.试问当地电价最低为多少时,可保证电力部门的收益比上年度至少增加20%.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,设动点P到定点F(1,0)的距离与到定直线l:x=﹣1的距离相等,记P的轨迹为Γ.又直线AB的一个方向向量 ![]() 且过点(1,0),AB与Γ交于A、B两点,求|AB|的长.
且过点(1,0),AB与Γ交于A、B两点,求|AB|的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com