练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f（2x-1）=4x2，则f（x）=________．

    x2+2x+1
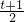
    分析：由题意，可用换元法求函数解析式，令t=2x-1得x=代入f（2x-1）=4x2，整理即可得到所求的函数解析式
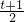
    解答：由题意，令t=2x-1得x=则
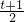
    f（t）=4（）2=t2+2t+1
    ∴f（x）=x2+2x+1
    故答案为x2+2x+1
    点评：本题考查函数解析式求解方法-换元法，掌握换元法的解题步骤及规则是解答本题的关键，换元法适用于已知复合函数解析式与内层函数解析式求外层函数解析式，其具体步骤是：先令内层函数g（x）=t，解出x=g-1（t），代入复合函数解析式，整理出关于t的函数，最后再将t换成x即可得到所求的解析式
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（2x-1）=x2，（x∈R），求f（x-1）的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    2x-1
    (x∈[2，6])    ，求函数的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•开封一模）已知函数f(x)=
    2x-1，(x≤0)
    f(x-1)+1，(x＞0)
    ，把函数g(x)=f(x)-x    的零点按从小到大的顺序排列成一个数列，则该数列的前n项的和为Sn，则S10=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    2x-1
    ．
    （1）用函数的单调性的定义证明f（x）在（1，+∞）上是减函数．
    （2）求函数f（x）在[2，6]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    2x-1  (x≥0)
    (
    1
    3
    )x    (x＜0)
    ，则f（f（-2））=
    17
    17
    ．

    查看答案和解析>>

    同步练习册答案