
设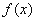 是定义在
是定义在 上的偶函数,
上的偶函数,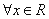 ,都有
,都有 ,且当
,且当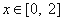 时,
时,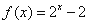 ,若函数
,若函数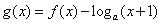
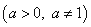 在区间
在区间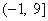 内恰有三个不同零点,则实数
内恰有三个不同零点,则实数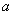 的取值范围是
的取值范围是
A.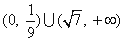 B.
B. 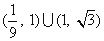
C. 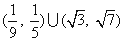 D.
D. 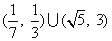
C 解析:由 ,得
,得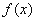 关于直线
关于直线 对称,
对称,
又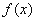 是定义在
是定义在 上的偶函数,
上的偶函数,


 ,即
,即 ,
,
所以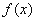 是周期为4的周期函数,
是周期为4的周期函数,
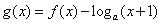 的零点即函数
的零点即函数 与
与 的交点,
的交点,
作出函数 的图像:
的图像:

①若 ,
,
当函数 经过点
经过点 时,函数
时,函数 与
与 有2个交点,
有2个交点,
此时 ,解得
,解得 ,
,
当函数 经过点
经过点 时,函数
时,函数 与
与 有4个交点,
有4个交点,
此时 ,解得
,解得 ,
,
要使两个函数有3个交点,则 ;
;
②若 ,
,
当函数 经过点
经过点 时,函数
时,函数 与
与 有2个交点,
有2个交点,
此时 ,解得
,解得 ,
,
当函数 经过点
经过点 时,函数
时,函数 与
与 有4个交点,
有4个交点,
此时 ,解得
,解得 ,
,
要使两个函数有3个交点,则 ,
,
综上,若函数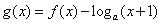
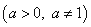 在区间
在区间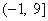 内恰有三个不同零点,则实数
内恰有三个不同零点,则实数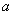 的取值范围是
的取值范围是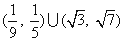 ,
,
故选:C
【思路点拨】根据条件确定函数的奇偶性和周期性,由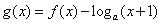
 ,得
,得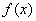
 ,在同一个坐标系内分别作出两个函数的图象,根据数形结合即可得到结论.
,在同一个坐标系内分别作出两个函数的图象,根据数形结合即可得到结论.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
设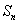 是数列
是数列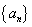 的前
的前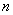 项和,对任意
项和,对任意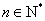 都有
都有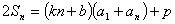 成立, (其中
成立, (其中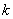 、
、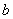 、
、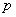 是常数) .
是常数) .
(1)当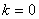 ,
,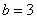 ,
,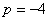 时,求
时,求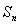 ;
;
(2)当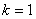 ,
,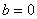 ,
,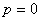 时,
时,
①若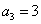 ,
,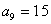 ,求数列
,求数列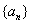 的通项公式;
的通项公式;
②设数列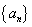 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“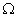 数列”.
数列”.
如果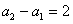 ,试问:是否存在数列
,试问:是否存在数列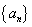 为“
为“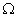 数列”,使得对任意
数列”,使得对任意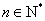 ,都有
,都有
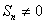 ,且
,且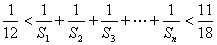 .若存在,求数列
.若存在,求数列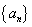 的首项
的首项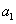 的所
的所
有取值构成的集合;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
据民生所望,相关部门对所属单位进行整治性核查,标准如下表:
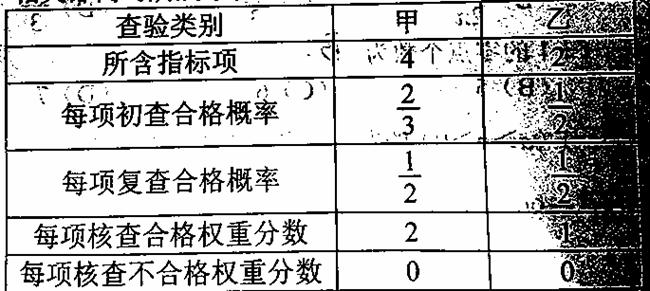
规定初查累计权重分数为10分或9分的不需要复查并给予奖励,10分的奖励18万元;9分的奖励8万元;初查累计权重分数为7分及其以下的停下运营并罚款1万元;初查累计权重分数为8分的要对不合格指标进行复查,最终累计权重得分等于初查合格部分与复查部分得分的和,最终累计权重分数为10分方可继续运营,否则停业运营并罚款1万元.
(1)求一家单位既没获奖励又没被罚款的概率;
(2)求一家单位在这次整治性核查中所获金额X(万元)的分布列和数学期望(奖励为正数,罚款为负数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com