练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，角A，B，C的对边分别为a，b，c．已知a2－c2＝2b，且sinB＝4cosAsinC，则b的值为(　　)

    A．4 B．8 C．6 D．10

     

    A

    【解析】由余弦定理，得a2－c2＝b2－2bccosA．

    ∵a2－c2＝2b，b≠0，∴b2－2bccosA＝2b，即b＝2ccosA＋2．由正弦定理及sinB＝4cosAsinC，得2cosA＝＝．∴b＝＋2，即b＝4．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：4-3平面向量的数量积及应用（解析版） 题型：选择题

    已知向量a，b的模都是2，其夹角为60°，又知＝3a＋2b，＝a＋3b，则P，Q两点间的距离为(　　)

    A．2 B． C．2 D．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：4-1向量的概念及运算（解析版） 题型：选择题

    设a、b都是非零向量，下列四个条件中，使＝成立的充分条件是(　　)

    A．|a|＝|b|且a∥b B．a＝－b

    C．a∥b D．a＝2b

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：3-8解三角形应用举例（解析版） 题型：选择题

    某人先向正东方向走了x km，然后他向右转150°，向新的方向走了3 km，结果他离出发点恰好为km，那么x的值为(　　)

    A． B．2 C．2或 D．3

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：3-7正弦定理和余弦定理（解析版） 题型：解答题

    在△ABC中，a，b，c分别是三内角A，B，C所对的三边，已知b2＋c2＝a2＋bc．

    (1)求角A的大小；

    (2)若2sin2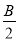＋2sin2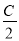＝1，试判断△ABC的形状．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：3-6简单的三角恒等变换（解析版） 题型：解答题

    在△ABC中，a，b，c分别是角A，B，C的对边，向量m＝(2sinB,2－cos2B)，n＝(2sin2(＋)，－1)，且m⊥n．

    (1)求角B的大小；

    (2)求sinA＋cosC的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：3-6简单的三角恒等变换（解析版） 题型：填空题

    设α，β∈(0，π)，且sin(α＋β)＝，tan＝，则cosβ的值为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：3-5两角和与差的正弦、余弦和正切（解析版） 题型：填空题

    已知α为锐角，且cos(α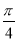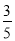＋)＝，则sinα＝________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-9函数模型及其应用（解析版） 题型：解答题

    某市居民自来水收费标准如下：每户每月用水不超过4吨时，每吨为1.80元，当用水超过4吨时，超过部分每吨3.00元，某月甲、乙两户共交水费y元，已知甲、乙两户该月用水量分别为5x吨、3x吨．

    (1)求y关于x的函数；

    (2)若甲、乙两户该月共交水费26.4元，分别求出甲、乙两户该月的用水量和水费．

     

    查看答案和解析>>

    同步练习册答案