
在△ABC中,a,b,c分别是角A,B,C的对边,向量m=(2sinB,2-cos2B),n=(2sin2( +
+ ),-1),且m⊥n.
),-1),且m⊥n.
(1)求角B的大小;
(2)求sinA+cosC的取值范围.
(1)B=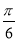 或B=
或B=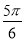
(2)(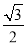 ,
,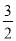 )
)
【解析】【解析】
(1)因为m⊥n,所以m·n=0,
所以2sinB·2sin2(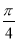 +
+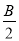 )-2+cos2B=0,
)-2+cos2B=0,
即2sinB·[1-cos2(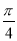 +
+ )]-2+cos2B=0,
)]-2+cos2B=0,
即2sinB+2sin2B-2+1-2sin2B=0,解得sinB=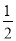 .
.
由于0<B<π,所以B=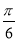 或B=
或B=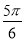 .
.
(2)当B=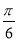 时,sinA+cosC=sinA+cos(
时,sinA+cosC=sinA+cos(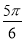 -A)=sinA-
-A)=sinA-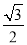 cosA+
cosA+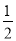 sinA=
sinA=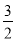 sinA-
sinA-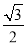 cosA=
cosA=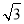 ×(
×(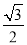 sinA-
sinA-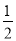 cosA)=
cosA)=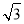 sin(A-
sin(A-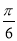 ).
).
由于0<A<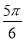 ,所以-
,所以-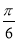 <A-
<A-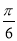 <
<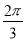 ,
,
所以-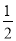 <sin(A-
<sin(A-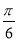 )≤1,
)≤1,
所以sinA+cosC的取值范围是(-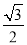 ,
,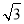 ];
];
当B=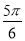 时,sinA+cosC=sinA+cos(
时,sinA+cosC=sinA+cos(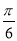 -A)=sinA+
-A)=sinA+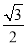 cosA+
cosA+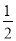 sinA=
sinA=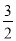 sinA+
sinA+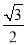 cosA=
cosA=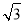 ×(
×(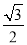 sinA+
sinA+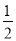 cosA)=
cosA)=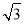 sin(A+
sin(A+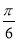 ),
),
由于0<A< ,故
,故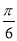 <A+
<A+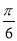 <
<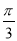 ,
,
故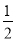 <sin(A+
<sin(A+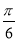 )<
)<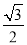 ,
,
所以sinA+cosC的取值范围是(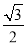 ,
,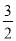 ).
).


科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-3平面向量的数量积及应用(解析版) 题型:填空题
在四边形ABCD中, =
=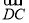 =(1,1),
=(1,1), ·
· +
+ ·
·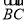 =
=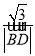 ·
· ,则四边形ABCD的面积为________.
,则四边形ABCD的面积为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:选择题
在平行四边形ABCD中,对角线AC=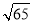 ,BD=
,BD=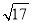 ,周长为18,则这个平行四边形的面积为( )
,周长为18,则这个平行四边形的面积为( )
A.16 B. C.18 D.32
C.18 D.32
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:解答题
在△ABC中,内角A,B,C的对边分别为a,b,c.已知cosA=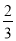 ,sinB=
,sinB=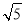 cosC.
cosC.
(1)求tanC的值;
(2)若a= ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:选择题
在△ABC中,角A,B,C的对边分别为a,b,c.已知a2-c2=2b,且sinB=4cosAsinC,则b的值为( )
A.4 B.8 C.6 D.10
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-6简单的三角恒等变换(解析版) 题型:解答题
已知函数f(x)=cos(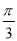 +x)·cos(
+x)·cos(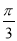 -x),g(x)=
-x),g(x)=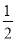 sin2x-
sin2x-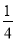 .
.
(1)求函数f(x)的最小正周期;
(2)求函数h(x)=f(x)-g(x)的最大值,并求使h(x)取得最大值的x的集合.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-6简单的三角恒等变换(解析版) 题型:选择题
若0<α<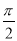 ,-
,-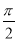 <β<0,cos(
<β<0,cos(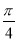 +α)=
+α)=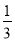 ,cos(
,cos(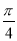 -
-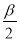 )=
)=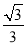 ,则cos(α+
,则cos(α+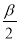 )=( )
)=( )
A.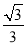 B.-
B.-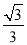 C.
C.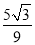 D.-
D.-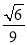
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-5两角和与差的正弦、余弦和正切(解析版) 题型:选择题
若sin( +α)=
+α)= ,则cos(
,则cos( -2α)等于( )
-2α)等于( )
A.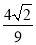 B.-
B.-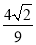 C.
C. D.-
D.-
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-9函数模型及其应用(解析版) 题型:选择题
某城市对一种售价为每件160元的商品征收附加税,税率为R%(即每销售100元征税R元),若年销售量为(30-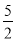 R)万件,要使附加税不少于128万元,则R的取值范围是( )
R)万件,要使附加税不少于128万元,则R的取值范围是( )
A.[4,8] B.[6,10] C.[4%,8%] D.[6%,100%]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com