
已知函数f(x)=cos(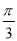 +x)·cos(
+x)·cos(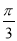 -x),g(x)=
-x),g(x)=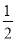 sin2x-
sin2x-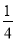 .
.
(1)求函数f(x)的最小正周期;
(2)求函数h(x)=f(x)-g(x)的最大值,并求使h(x)取得最大值的x的集合.
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-3平面向量的数量积及应用(解析版) 题型:选择题
设O点在△ABC内部,且有 +
+ +2
+2 =0,则△ABC的面积与△AOC的面积的比值为( )
=0,则△ABC的面积与△AOC的面积的比值为( )
A.4 B. C.2
C.2 D.3
D.3
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:填空题
一角槽的断面如图,四边形ADEB是矩形,若α=50°,β=70°,AC=90 mm,BC=150 mm,则DE的长度等于________ mm.

查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:填空题
在△ABC中,设角A、B、C的对边分别为a、b、c,若a=(cosC,2a-c),b=(b,-cosB)且a⊥b,则B=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-6简单的三角恒等变换(解析版) 题型:解答题
在△ABC中,a,b,c分别是角A,B,C的对边,向量m=(2sinB,2-cos2B),n=(2sin2( +
+ ),-1),且m⊥n.
),-1),且m⊥n.
(1)求角B的大小;
(2)求sinA+cosC的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-6简单的三角恒等变换(解析版) 题型:选择题
已知cos(α-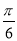 )+sinα=
)+sinα=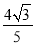 ,则sin(α+
,则sin(α+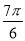 )的值是( )
)的值是( )
A.-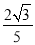 B.
B.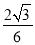 C.-
C.-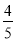 D.
D.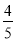
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-5两角和与差的正弦、余弦和正切(解析版) 题型:选择题
已知α,β∈(0,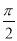 ),满足tan(α+β)=4tanβ,则tanα的最大值是( )
),满足tan(α+β)=4tanβ,则tanα的最大值是( )
A.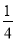 B.
B.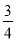 C.
C.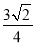 D.
D.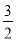
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:解答题
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,- <φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).
<φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).

(1)求函数f(x)的解析式;
(2)若锐角θ满足cosθ= ,求f(2θ)的值.
,求f(2θ)的值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-8函数与方程(解析版) 题型:解答题
已知函数f(x)=-x2+2ex+m-1,g(x)=x+ (x>0).
(x>0).
(1)若g(x)=m有实数根,求m的取值范围;
(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com