
已知函数f(x)=-x2+2ex+m-1,g(x)=x+ (x>0).
(x>0).
(1)若g(x)=m有实数根,求m的取值范围;
(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.
(1)m≥2e
(2)(-e2+2e+1,+∞)
【解析】【解析】
(1)∵g(x)=x+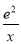 ≥2
≥2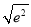 =2e等号成立的条件是x=e,故g(x)的值域是[2e,+∞),因此,只需m≥2e,g(x)=m就有实数根.
=2e等号成立的条件是x=e,故g(x)的值域是[2e,+∞),因此,只需m≥2e,g(x)=m就有实数根.

(2)若g(x)-f(x)=0有两个相异的实根,即g(x)与f(x)的图象有两个不同的交点,作出g(x)与f(x)的大致图象.
∵f(x)=-x2+2ex+m-1=-(x-e)2+m-1+e2,
∴其图象的对称轴为x=e,开口向下,最大值为m-1+e2.
故当m-1+e2>2e,即m>-e2+2e+1时,g(x)与f(x)有两个交点,
即g(x)-f(x)=0有两个相异实根.
∴m的取值范围是(-e2+2e+1,+∞).


 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-6简单的三角恒等变换(解析版) 题型:解答题
已知函数f(x)=cos(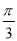 +x)·cos(
+x)·cos(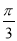 -x),g(x)=
-x),g(x)=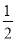 sin2x-
sin2x-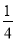 .
.
(1)求函数f(x)的最小正周期;
(2)求函数h(x)=f(x)-g(x)的最大值,并求使h(x)取得最大值的x的集合.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:填空题
已知函数f(x)=sinx+ cosx(x∈R),函数y=f(x+φ)(|φ|≤
cosx(x∈R),函数y=f(x+φ)(|φ|≤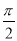 )的图象关于直线x=0对称,则φ的值为________.
)的图象关于直线x=0对称,则φ的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-9函数模型及其应用(解析版) 题型:解答题
某书商为提高某套丛书的销量,准备举办一场展销会.据市场调查,当每套丛书售价定为x元时,销售量可达到15—0.1x万套.现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10.假设不计其他成本,即销售每套丛书的利润=售价-供货价格.问:
(1)每套丛书售价定为100元时,书商能获得的总利润是多少万元?
(2)每套丛书售价定为多少元时,单套丛书的利润最大?
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-9函数模型及其应用(解析版) 题型:选择题
某城市对一种售价为每件160元的商品征收附加税,税率为R%(即每销售100元征税R元),若年销售量为(30-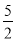 R)万件,要使附加税不少于128万元,则R的取值范围是( )
R)万件,要使附加税不少于128万元,则R的取值范围是( )
A.[4,8] B.[6,10] C.[4%,8%] D.[6%,100%]
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-8函数与方程(解析版) 题型:解答题
是否存在这样的实数a,使函数f(x)=x2+(3a-2)x+a-1在区间[-1,3]上恒有一个零点,且只有一个零点?若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-7函数的图象(解析版) 题型:选择题
在函数y=|x|(x∈[-1,1])的图象上有一点P(t,|t|),此函数与x轴、直线x=-1及x=t围成图形(如图阴影部分)的面积为S,则S与t的函数关系图象可表示为( )
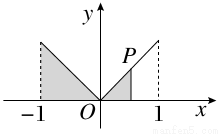
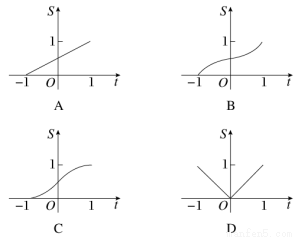
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-4二次函数与幂函数(解析版) 题型:选择题
设函数f(x)=-2x2+4x在区间[m,n]上的值域是[-6,2],则m+n的取值所组成的集合为( )
A.[0,3] B.[0,4] C.[-1,3] D.[1,4]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com