
是否存在这样的实数a,使函数f(x)=x2+(3a-2)x+a-1在区间[-1,3]上恒有一个零点,且只有一个零点?若存在,求出a的取值范围;若不存在,说明理由.
a的取值范围为a>1或a<-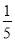
【解析】【解析】
令f(x)=0,则Δ=(3a-2)2-4(a-1)=9a2-16a+8=9(a-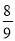 )2+
)2+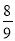 >0,即f(x)=0有两个不相等的实数根,
>0,即f(x)=0有两个不相等的实数根,
∴若实数a满足条件,则只需f(-1)·f(3)≤0即可.
f(-1)·f(3)=(1-3a+2+a-1)·(9+9a-6+a-1)=4(1-a)(5a+1)≤0,
∴a≤-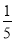 或a≥1.
或a≥1.
检验:(1)当f(-1)=0时,a=1,所以f(x)=x2+x.
令f(x)=0,即x2+x=0,得x=0或x=-1.
方程在[-1,3]上有两个实数根,不合题意,故a≠1.
当f(3)=0时,a=-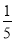 ,
,
此时f(x)=x2-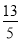 x-
x-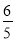 .
.
令f(x)=0,即x2-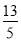 x-
x-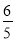 =0,
=0,
解得x=-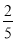 或x=3.
或x=3.
方程在[-1,3]上有两个实数根,不合题意,故a≠-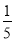 .
.
所以a的取值范围为a>1或a<-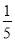 .
.


科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-6简单的三角恒等变换(解析版) 题型:选择题
已知cos(α-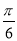 )+sinα=
)+sinα=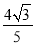 ,则sin(α+
,则sin(α+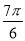 )的值是( )
)的值是( )
A.-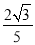 B.
B.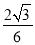 C.-
C.-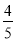 D.
D.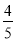
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:解答题
已知函数f(x)=Asin(ωx+φ)+1(ω>0,A>0,0<φ<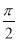 )的周期为π,f(
)的周期为π,f(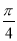 )=
)=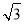 +1,且f(x)的最大值为3.
+1,且f(x)的最大值为3.
(1)写出f(x)的表达式;
(2)写出函数f(x)的对称中心,对称轴方程.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-9函数模型及其应用(解析版) 题型:填空题
某厂去年的产值为1,若计划在今后五年内每年的产值比上年增长10%,则从今年起到第五年这五年内,这个厂的总产值约为________.(保留一位小数,取1.15≈1.6)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-8函数与方程(解析版) 题型:解答题
已知函数f(x)=-x2+2ex+m-1,g(x)=x+ (x>0).
(x>0).
(1)若g(x)=m有实数根,求m的取值范围;
(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-8函数与方程(解析版) 题型:选择题
函数f(x)=lnx-x-a有两个不同的零点,则实数a的取值范围是( )
A.(-∞,-1] B.(-∞,-1)
C.[-1,+∞) D.(-1,+∞)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-7函数的图象(解析版) 题型:填空题
给出定义:若m-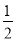 <x≤m+
<x≤m+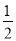 (其中m为整数),则m叫做离实数x最近的整数,记作{x}=m,在此基础上给出下列关于函数f(x)=|x-{x}|的四个命题:①函数y=f(x)的定义域为R,值域为[0,
(其中m为整数),则m叫做离实数x最近的整数,记作{x}=m,在此基础上给出下列关于函数f(x)=|x-{x}|的四个命题:①函数y=f(x)的定义域为R,值域为[0,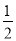 ];②函数y=f(x)在[-
];②函数y=f(x)在[-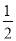 ,
,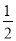 ]上是增函数;③函数y=f(x)是周期函数,最小正周期为1;④函数y=f(x)的图象关于直线x=
]上是增函数;③函数y=f(x)是周期函数,最小正周期为1;④函数y=f(x)的图象关于直线x= (k∈Z)对称.其中正确命题的序号是________.
(k∈Z)对称.其中正确命题的序号是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-6对数与对数函数(解析版) 题型:选择题
设a=lg e,b=(lg e)2,c=lg ,则( )
,则( )
A.a>b>c B.a>c>b
C.c>a>b D.c>b>a
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-3函数的奇偶性与周期性(解析版) 题型:解答题
已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,又f(1)=-2.
(1)判断f(x)的奇偶性;
(2)求证:f(x)是R上的减函数;
(3)求f(x)在区间[-3,3]上的值域;
(4)若?x∈R,不等式f(ax2)-2f(x)<f(x)+4恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com