
已知函数f(x)=Asin(ωx+φ)+1(ω>0,A>0,0<φ<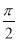 )的周期为π,f(
)的周期为π,f(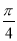 )=
)=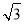 +1,且f(x)的最大值为3.
+1,且f(x)的最大值为3.
(1)写出f(x)的表达式;
(2)写出函数f(x)的对称中心,对称轴方程.
 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:选择题
要测量底部不能到达的东方明珠电视塔的高度,在黄埔江西岸选择C、D两观测点,在C、D两点测得塔顶的仰角分别为45°,30°,在水平面上测得电视塔底与C地连线及C、D两地连线所成的角为120°,C、D两地相距500 m,则电视塔的高度是( )
A.100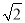 m B.400 m C.200
m B.400 m C.200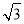 m D.500 m
m D.500 m
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-5两角和与差的正弦、余弦和正切(解析版) 题型:填空题
已知函数f(x)=2cosx(sinx-cosx)+1,x∈R,则函数f(x)在区间[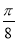 ,
,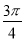 ]上的最大值和最小值分别为________.
]上的最大值和最小值分别为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:选择题
已知函数f(x)=Asin(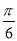 x+φ)(A>0,0<φ<
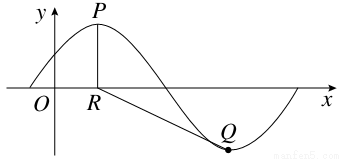
x+φ)(A>0,0<φ<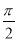 )的部分图象如图所示,P,Q分别为该图象的最高点和最低点,点P的坐标为(2,A),点R的坐标为(2,0).若∠PRQ=
)的部分图象如图所示,P,Q分别为该图象的最高点和最低点,点P的坐标为(2,A),点R的坐标为(2,0).若∠PRQ=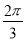 ,则y=f(x)的最大值及φ的值分别是( )
,则y=f(x)的最大值及φ的值分别是( )
A.2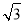 ,
,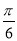 B.
B.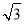 ,
,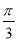
C.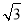 ,
,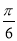 D.2
D.2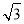 ,
,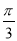
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:填空题
已知函数f(x)=sinx+ cosx(x∈R),函数y=f(x+φ)(|φ|≤
cosx(x∈R),函数y=f(x+φ)(|φ|≤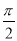 )的图象关于直线x=0对称,则φ的值为________.
)的图象关于直线x=0对称,则φ的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:选择题
函数f(x)= cos(ωx+φ)对任意的x∈R,都有f(
cos(ωx+φ)对任意的x∈R,都有f(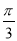 -x)=f(
-x)=f(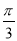 +x),若函数g(x)=3sin(ωx+φ)-2,则g(
+x),若函数g(x)=3sin(ωx+φ)-2,则g(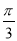 )的值是( )
)的值是( )
A.1 B.-5或3 C.-2 D.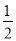
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-9函数模型及其应用(解析版) 题型:解答题
某书商为提高某套丛书的销量,准备举办一场展销会.据市场调查,当每套丛书售价定为x元时,销售量可达到15—0.1x万套.现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10.假设不计其他成本,即销售每套丛书的利润=售价-供货价格.问:
(1)每套丛书售价定为100元时,书商能获得的总利润是多少万元?
(2)每套丛书售价定为多少元时,单套丛书的利润最大?
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-8函数与方程(解析版) 题型:解答题
是否存在这样的实数a,使函数f(x)=x2+(3a-2)x+a-1在区间[-1,3]上恒有一个零点,且只有一个零点?若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-5指数及指数函数(解析版) 题型:解答题
定义在[-1,1]上的奇函数f(x),已知当x∈[-1,0]时,
f(x)=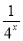 -
-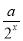 (a∈R).
(a∈R).
(1)求f(x)在[0,1]上的最大值;
(2)若f(x)是[0,1]上的增函数,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com