
已知函数f(x)=Asin(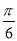 x+φ)(A>0,0<φ<
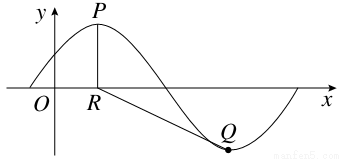
x+φ)(A>0,0<φ<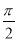 )的部分图象如图所示,P,Q分别为该图象的最高点和最低点,点P的坐标为(2,A),点R的坐标为(2,0).若∠PRQ=
)的部分图象如图所示,P,Q分别为该图象的最高点和最低点,点P的坐标为(2,A),点R的坐标为(2,0).若∠PRQ=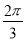 ,则y=f(x)的最大值及φ的值分别是( )
,则y=f(x)的最大值及φ的值分别是( )
A.2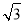 ,
,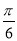 B.
B.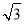 ,
,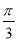
C.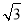 ,
,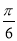 D.2
D.2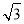 ,
,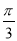
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:解答题
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-6简单的三角恒等变换(解析版) 题型:选择题
已知cos(α-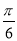 )+sinα=
)+sinα=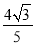 ,则sin(α+
,则sin(α+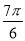 )的值是( )
)的值是( )
A.-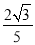 B.
B.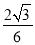 C.-
C.-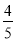 D.
D.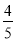
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-5两角和与差的正弦、余弦和正切(解析版) 题型:选择题
已知cosα=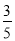 ,cos(α+β)=-
,cos(α+β)=-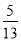 ,α,β都是锐角,则cosβ=( )
,α,β都是锐角,则cosβ=( )
A.-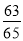 B.-
B.-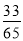 C.
C.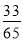 D.
D.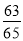
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:解答题
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,- <φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).
<φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).

(1)求函数f(x)的解析式;
(2)若锐角θ满足cosθ= ,求f(2θ)的值.
,求f(2θ)的值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:选择题
将函数f(x)=sin(2x+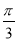 )的图象向左平移φ个单位,得到偶函数g(x)的图象,则φ的最小正值为( )
)的图象向左平移φ个单位,得到偶函数g(x)的图象,则φ的最小正值为( )
A.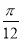 B.
B.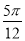 C.
C.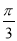 D.
D.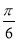
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:解答题
已知函数f(x)=Asin(ωx+φ)+1(ω>0,A>0,0<φ<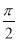 )的周期为π,f(
)的周期为π,f(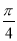 )=
)=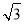 +1,且f(x)的最大值为3.
+1,且f(x)的最大值为3.
(1)写出f(x)的表达式;
(2)写出函数f(x)的对称中心,对称轴方程.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-9函数模型及其应用(解析版) 题型:填空题
某厂去年的产值为1,若计划在今后五年内每年的产值比上年增长10%,则从今年起到第五年这五年内,这个厂的总产值约为________.(保留一位小数,取1.15≈1.6)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-6对数与对数函数(解析版) 题型:选择题
设a=lg e,b=(lg e)2,c=lg ,则( )
,则( )
A.a>b>c B.a>c>b
C.c>a>b D.c>b>a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com