
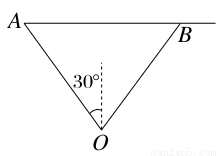
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
(1)当t=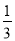 时,Smin=10
时,Smin=10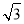 ,此时v=
,此时v=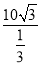 =30
=30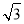
(2)航行方向为北偏东30°,航行速度为30海里/小时,小艇能以最短时间与轮船相遇.
【解析】【解析】
(1)设相遇时小艇航行的距离为S海里,则
S=
=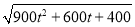
=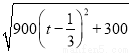 .
.
故当t=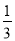 时,Smin=10
时,Smin=10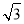 ,此时v=
,此时v=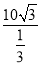 =30
=30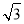 .
.
答:小艇以30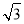 海里/小时的速度航行,相遇时小艇的航行距离最小.
海里/小时的速度航行,相遇时小艇的航行距离最小.
(2)设小艇与轮船在B处相遇,如图,则v2t2=400+900t2-2·20·30t·cos(90°-30°),
故v2=900-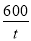 +
+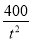 .
.
∵0<v≤30,∴900-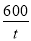 +
+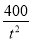 ≤900,即
≤900,即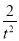 -
-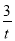 ≤0,
≤0,
解得t≥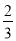 .
.
又t= 时,v=30.
时,v=30.
故v=30时,t取最小值,且最小值等于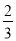 .
.
此时,在△OAB中,有OA=OB=AB=20,故可设计航行方案如下:
航行方向为北偏东30°,航行速度为30海里/小时,小艇能以最短时间与轮船相遇.


科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-1数列的概念与简单表示法(解析版) 题型:解答题
已知数列{an}满足:a1=1,2n-1an=an-1(n∈N*,n≥2).
(1)求数列{an}的通项公式;
(2)这个数列从第几项开始及以后各项均小于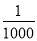 ?
?
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-2平面向量的基本定理及坐标表示(解析版) 题型:填空题
若等边三角形ABC的边长为2 ,平面内一点M满足
,平面内一点M满足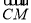 =
=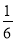
 +
+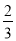
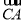 ,则
,则 ·
·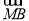 =________.
=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-1向量的概念及运算(解析版) 题型:选择题
BC是单位圆A的一条直径,F是线段AB上的点,且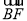 =2
=2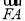 ,若DE是圆A中绕圆心A运动的一条直径,则
,若DE是圆A中绕圆心A运动的一条直径,则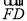 ·
·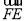 的值是( )
的值是( )
A.-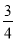 B.-
B.-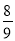 C.-
C.-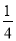 D.不确定
D.不确定
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-1向量的概念及运算(解析版) 题型:选择题
在梯形ABCD中,AB∥CD,AB=2CD,M、N分别为CD、BC的中点,若 =λ
=λ +μ
+μ ,则λ+μ=( )
,则λ+μ=( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:解答题
如图,A,B是海面上位于东西方向相距5(3+ )海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?

查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:选择题
要测量底部不能到达的东方明珠电视塔的高度,在黄埔江西岸选择C、D两观测点,在C、D两点测得塔顶的仰角分别为45°,30°,在水平面上测得电视塔底与C地连线及C、D两地连线所成的角为120°,C、D两地相距500 m,则电视塔的高度是( )
A.100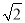 m B.400 m C.200
m B.400 m C.200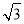 m D.500 m
m D.500 m
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:选择题
已知在锐角△ABC中,角A,B,C所对的边分别为a,b,c,且tanC=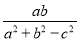 ,则角C为( )
,则角C为( )
A. B.
B.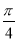 C.
C.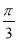 D.
D.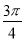
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:选择题
已知函数f(x)=Asin(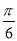 x+φ)(A>0,0<φ<
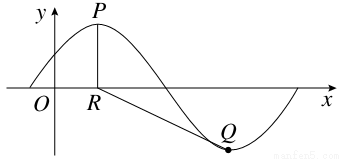
x+φ)(A>0,0<φ<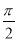 )的部分图象如图所示,P,Q分别为该图象的最高点和最低点,点P的坐标为(2,A),点R的坐标为(2,0).若∠PRQ=
)的部分图象如图所示,P,Q分别为该图象的最高点和最低点,点P的坐标为(2,A),点R的坐标为(2,0).若∠PRQ=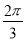 ,则y=f(x)的最大值及φ的值分别是( )
,则y=f(x)的最大值及φ的值分别是( )
A.2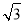 ,
,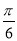 B.
B.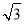 ,
,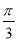
C.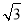 ,
,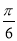 D.2
D.2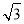 ,
,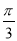
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com