
在△ABC中,设角A、B、C的对边分别为a、b、c,若a=(cosC,2a-c),b=(b,-cosB)且a⊥b,则B=________.
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-3平面向量的数量积及应用(解析版) 题型:解答题
在△ABC中,已知2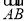 ·
·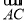 =
=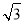 |
|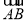 |·|
|·|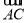 |=3|
|=3|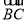 |2,求角A,B,C的大小.
|2,求角A,B,C的大小.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-1向量的概念及运算(解析版) 题型:选择题
在梯形ABCD中,AB∥CD,AB=2CD,M、N分别为CD、BC的中点,若 =λ
=λ +μ
+μ ,则λ+μ=( )
,则λ+μ=( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:选择题
要测量底部不能到达的东方明珠电视塔的高度,在黄埔江西岸选择C、D两观测点,在C、D两点测得塔顶的仰角分别为45°,30°,在水平面上测得电视塔底与C地连线及C、D两地连线所成的角为120°,C、D两地相距500 m,则电视塔的高度是( )
A.100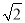 m B.400 m C.200
m B.400 m C.200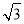 m D.500 m
m D.500 m
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:解答题
在△ABC中,内角A,B,C的对边分别为a,b,c.已知cosA=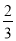 ,sinB=
,sinB=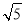 cosC.
cosC.
(1)求tanC的值;
(2)若a= ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:选择题
已知在锐角△ABC中,角A,B,C所对的边分别为a,b,c,且tanC=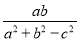 ,则角C为( )
,则角C为( )
A. B.
B.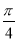 C.
C.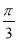 D.
D.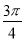
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-6简单的三角恒等变换(解析版) 题型:解答题
已知函数f(x)=cos(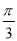 +x)·cos(
+x)·cos(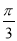 -x),g(x)=
-x),g(x)=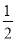 sin2x-
sin2x-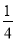 .
.
(1)求函数f(x)的最小正周期;
(2)求函数h(x)=f(x)-g(x)的最大值,并求使h(x)取得最大值的x的集合.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-5两角和与差的正弦、余弦和正切(解析版) 题型:填空题
已知函数f(x)=2cosx(sinx-cosx)+1,x∈R,则函数f(x)在区间[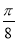 ,
,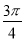 ]上的最大值和最小值分别为________.
]上的最大值和最小值分别为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-9函数模型及其应用(解析版) 题型:解答题
某书商为提高某套丛书的销量,准备举办一场展销会.据市场调查,当每套丛书售价定为x元时,销售量可达到15—0.1x万套.现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10.假设不计其他成本,即销售每套丛书的利润=售价-供货价格.问:
(1)每套丛书售价定为100元时,书商能获得的总利润是多少万元?
(2)每套丛书售价定为多少元时,单套丛书的利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com