
(本小题满分14分)已知函数 的导函数是
的导函数是 ,
, 在
在 处取得极值,且
处取得极值,且 ,
,
(1)求 的极大值和极小值;
的极大值和极小值;
(2)记 在闭区间
在闭区间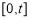 上的最大值为
上的最大值为 ,若对任意的
,若对任意的
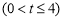 总有
总有
 成立,求
成立,求 的取值范围;
的取值范围;
(Ⅲ)设 是曲线
是曲线 上的任意一点.当
上的任意一点.当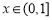 时,求直线OM斜率的最小值,据此判断
时,求直线OM斜率的最小值,据此判断 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.
(1)极大值为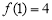 ,极小值为
,极小值为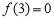 ;(2)
;(2)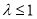 ;(Ⅲ)直线
;(Ⅲ)直线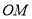 斜率的最小值为4,
斜率的最小值为4,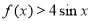 ,理由祥见解析.
,理由祥见解析.
【解析】
试题分析:(1)依题意,f'(3)=0,解得m=-6,由已知可设f(x)=x3-6x2+9x+p,因为f(0)=0,所以p=0,由此能求出f(x)的极大值和极小值.
(2)当0<t≤1时,由(1)知f(x)在[0,t]上递增,所以f(x)的最大值F(t)=f(t)=t3-6t2+9t,由F(t)≥λt对任意的t恒成立,得t3-6t2+9t≥λt,则λ≤t2-6t+9=(t-3)2,由此能求出λ的取值范围.
(Ⅲ)当x∈(0,1]时,直线OM斜率,因为0<x≤1,所以-3<x-3≤-2,则4≤(x-3)2<9,即直线OM斜率的最小值为4.由此能够导出f(x)>4s1nx.
试题解析: (1)依题意,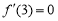 ,解得
,解得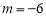 , 1分
, 1分
由已知可设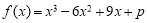 ,
,
因为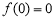 ,所以
,所以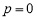 ,
,
则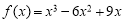 ,导函数
,导函数 . 3分
. 3分
列表:
|
| 1 | (1,3) | 3 | (3,+∞) |
| + | 0 | - | 0 | + |
| 递增 | 极大值4 | 递减 | 极小值0 | 递增 |
由上表可知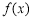 在
在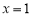 处取得极大值为
处取得极大值为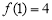 ,
,
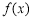 在
在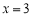 处取得极小值为
处取得极小值为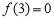 . 5分
. 5分
(2)①当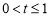 时,由(1)知
时,由(1)知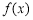 在
在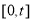 上递增,
上递增,
所以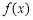 的最大值
的最大值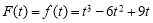 , 6分
, 6分
由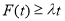 对任意的
对任意的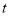 恒成立,得
恒成立,得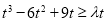 ,
,
则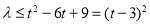 ,因为
,因为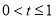 ,所以
,所以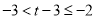 ,则
,则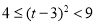 ,
,
因此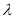 的取值范围是
的取值范围是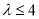 . 8分
. 8分
②当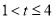 时,因为
时,因为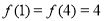 ,所以
,所以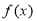 的最大值
的最大值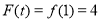 ,
,
由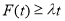 对任意的
对任意的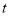 恒成立,得
恒成立,得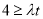 , ∴
, ∴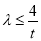 ,
,
因为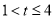 ,所以
,所以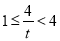 ,因此
,因此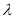 的取值范围是
的取值范围是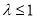 , 9分
, 9分
综上①②可知,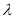 的取值范围是
的取值范围是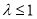 . 10分
. 10分
(Ⅲ)当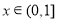 时,直线
时,直线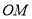 斜率
斜率 ,
,
因为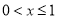 ,所以
,所以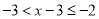 ,则
,则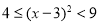 ,
,
即直线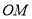 斜率的最小值为4. 11分
斜率的最小值为4. 11分
首先,由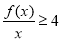 ,得
,得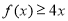 .
.
其次,当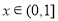 时,有
时,有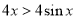 ,所以
,所以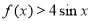 , 12分
, 12分
证明如下:
记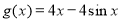 ,则
,则 ,
,
所以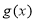 在
在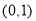 递增,又
递增,又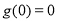 ,
,
则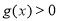 在
在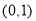 恒成立,即
恒成立,即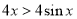 ,所以
,所以 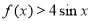 . 14分
. 14分
考点:1. 利用导数求闭区间上函数的最值;2. 利用导数研究函数的极值.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源:2015届辽宁省五校协作体高三上学期期中考试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-5:不等式选讲
已知函数 ,
,
(1)当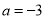 时,求不等式
时,求不等式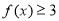 的解集;
的解集;
(2)若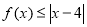 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届西藏拉萨中学高三第三次月考文科数学试卷(解析版) 题型:选择题
已知数列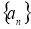 是等比数列,
是等比数列, 是其前
是其前 项和,且
项和,且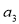 =2,
=2,  ,则
,则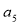 =
=
A.2或- B.
B.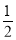 或-2 C.
或-2 C. D.2或
D.2或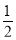
查看答案和解析>>
科目:高中数学 来源:2015届福建省福州市高三上学期第三次质检理科数学试卷(解析版) 题型:填空题
直线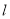 与函数
与函数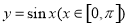 的图像相切于点
的图像相切于点 ,且
,且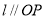 ,
, 为坐标原点,
为坐标原点,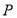 为图像的极大值点,
为图像的极大值点,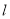 与
与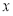 轴交于点
轴交于点 ,过切点
,过切点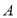 作
作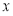 轴的垂线,垂足为
轴的垂线,垂足为 ,则
,则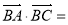 =__________.
=__________.
查看答案和解析>>
科目:高中数学 来源:2015届福建省福州市高三上学期第三次质检理科数学试卷(解析版) 题型:选择题
已知函数 的图像在点
的图像在点 处的切线
处的切线 与直线
与直线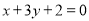 垂直,若数列
垂直,若数列 的前
的前 项和为
项和为 ,则
,则 的值为
的值为
A.  B.
B. 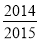 C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2015届福建省等三校高三上学期期中联考理科数学试卷(解析版) 题型:解答题
(本题满分13分)已知 ,
, .
.
(1)若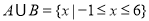 ,求实数
,求实数 的值;
的值;
(2)若“ ”是“
”是“ ”的充分不必要条件,求实数
”的充分不必要条件,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com